Weaver, Warren

A kommunikáció egy matematikai modellje^*

Hogyan kommunikálnak egymással az emberek? A közvetlenül vagy a telefonon, vagy a rádión keresztül kimondott szó; a kézzel, a postán, a távírón vagy bármilyen más módon továbbított írott vagy nyomtatott szó – mindezek a kommunikáció nyilvánvaló és közismert formái. De van sok egyéb is. Egy bólintás vagy egy intés, egy bőgés az őserdőbe, egy mozdulat a televízió képernyőjén, egy fényjel felvillanása, valamilyen múltbeli eseményre emlékeztető néhány zenei taktus, a levegőbe emelkedő füstoszlop, a mozdulatok és a testtartások a balettban – mindezekkel az eszközökkel az emberek gondolatokat továbbítanak.

Mi itt ennek megfelelően egészen tág értelemben használjuk a kommunikáció szót, olyan módon, hogy az magába foglalja mindazokat a folyamatokat, amelyek révén egyik tudat érintkezésbe léphet a másikkal. Habár szóhasználatunk sok esetben közvetlenül csak a beszéd útján való kommunikációra utal, gyakorlatilag mindaz, amit mondunk, ugyanúgy érvényes a zenére, a képekre és az információtovábbítás számos egyéb módszerére is.

Úgy tűnik, hogy a kommunikációval kapcsolatban három szinten jelentkeznek a problémák: 1. technikai, 2. szemantikai és 3. befolyásolási szinten.

A technikai problémák azzal kapcsolatosak, hogy mennyire pontosan kerül az információ az adótól a vevőhöz. Ezek a problémák jelen vannak a kommunikáció minden formájában, legyen az diszkrét szimbólumok sorozata (írott beszéd), váltakozó szignál (hangnak vagy zenének továbbítása telefonon vagy rádión keresztül) vagy váltakozó kétdimenziós struktúra (televízió).

A szemantikai problémák azzal kapcsolatosak, hogy a vevő jelentésértelmezése mennyire azonos az adó által szándékolt jelentéssel. Ez rendkívül mély és bonyolult szituáció, még ha csupán a beszédbeli kommunikáció viszonylag egyszerűbb problémáival foglalkozunk is. Így például, ha X-szel kapcsolatban felmerül az a gyanú, hogy nem érti azt, amit Y mond, akkor – amennyiben Y semmi egyebet nem tesz, mint tovább beszél X-szel – lehetetlen, hogy ez a helyzet véges időn belül tökéletesen tisztázódjék. Ha Y felteszi a kérdést: “Ért Ön engem?”, s X így válaszol: “feltétlenül”, ez még nem bizonyítéka annak, hogy a megértés létrejött. Nagyon is lehetséges, hogy X ezt a kérdést sem értette. Ha ez így kissé ostobán hangzik, képzeljük el ebben a formában: “Czy pan mnie rozumie?” –, amire ez a válasz: “hai wakatte imasu”. A beszédbeli kommunikáció korlátozott területén a nehézség tűrhető mértékűre csökkenthető (de tökéletesen soha meg nem szüntethető) “magyarázkodás” segítségével. Igaz ugyan, hogy a magyarázkodás mindig csak a megmagyarázandó gondolatok megközelítését jelenti, mindazonáltal érthető lesz, ha olyan nyelven hangzik el, amelyet a megelőző használat révén már kellő mértékben tisztáztak. Így pl. nem tart túl sokáig, hogy az “igen”-nek megfelelő szimbólumot bármilyen nyelven érthetővé tegyük.

A befolyásolás vagy hatékonyság problémái azzal kapcsolatosak, hogy a vevőhöz eljuttatott jelentés milyen sikerrel idézi elő a kívánt viselkedést. Első pillantásra túlzottan szűk horizontúnak tűnhet ez a felfogás, hogy minden kommunikáció célja befolyásolni a vevő viselkedését. Ám ha elég tágan definiáljuk a viselkedés fogalmát, akkor világos, hogy a kommunikáció vagy befolyásolja a viselkedést, vagy nincs semmiféle megállapítható és kimutatható hatása.

Hajlamosak vagyunk azt gondolni, hogy a technikai problémák körébe csak a kommunikációs rendszer jó megtervezésével összefüggő technikai részletek tartoznak, a kommunikáció általános problémájának filozófiai tartalmát pedig úgyszólván teljes egészében a szemantikai és hatékonysági problémák ölelik fel. Ahhoz, hogy világosan lássuk, mennyire nem így van, szemügyre kell vennünk bizonyos újabb fejleményeket a matematikai kommunikációelmélet területén.

Korántsem minden ízében új elméletről van szó. Amint arra Neumann János matematikus rámutatott, már Ludwig Boltzmann XIX. századi osztrák fizikus felvetette azt a gondolatot, hogy a statisztikai mechanika bizonyos fogalmai alkalmazhatók az információ fogalmára. A probléma kidolgozásához jelentősen hozzájárultak más tudósok is, főleg Norbert Wiener (Massachusetts Institute of Technology). Az, amiről itt szeretnénk beszámolni, Claude Shannon munkája (Belle Telephone Laboratories). Ennek a közvetlen előzménye ugyanennél az intézetnél H. Nyquist és R. V. L. Hartley munkája volt. Első megközelítésben csak a technikai problémára vonatkozik, de az elméletnek tágabb az érvényessége. Először is, a jelentést és a hatékonyságot elkerülhetetlenül korlátozzák a szimbólumtovábbítás pontosságának elméleti korlátai. Még ennél is fontosabb azonban az, hogy a technikai probléma elméleti elemzésekor kiderül: ez a probléma sokkal nagyobb mértékben átfedi a szemantikai és a hatékonysági problémákat, mint ahogyan azt gondolnánk.

Az 1. ábra szimbolikusan ábrázol egy kommunikációs rendszert. Az információforrás a lehetséges közlemények egy sorozatából kiválasztja a kívánt közleményt. (Látjuk majd, hogy ez a funkció különösen fontos.) Ezt a közleményt a továbbító átalakítja azzá a jellé [signal], amely áthalad a kommunikációs csatornán a vevőhöz.

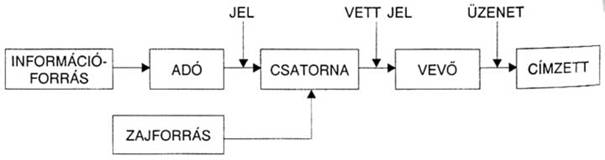
1. ábra

Egy kommunikációs rendszer ezekre az alapelemekre redukálható. A telefonban a jel a váltakozó elektromos áram, a csatorna pedig a kábel. A beszédnél a jel a váltakozó hangnyomás, a csatorna a levegő. A jelre sokszor az információforrás által nem kívánt dolgok is rárakódnak. Ilyen a rádió esetében a zörej, a telefonban a hang torzulása. Minden ilyen többletet zajnak nevezhetünk.

A vevő afféle fordított továbbító, amely a továbbított jelet visszaalakítja közleménnyé, s ezt a közleményt “kikézbesíti” rendeltetési helyére. Ha beszélek valakivel, az én agyam az információforrás, az övé a rendeltetési hely; hangberendezésem a továbbító, az ő füle és a hozzá kapcsolódó nyolcadik ideggel pedig a vevő.

A továbbítási folyamat sajnálatos jellegzetessége az, hogy a jelhez hozzáadódnak bizonyos dolgok, amelyeket az információforrásnak nem állt szándékában továbbítania. Ilyen nem kívánt többlet lehet a hang torzulása (pl. a telefonban) vagy a zörej (a rádióban), a kép alakjának vagy kontrasztjának torzulása (a televízióban), vagy hiba a továbbításban (távíró vagy fotókópia). A jel minden ilyen megváltozását zajnak nevezzük.

A kommunikációs rendszerben megvizsgálandó kérdések az információ mennyiségével, a kommunikációs csatorna kapacitásával, a közlemények jellé való átalakításakor alkalmazandó kódolási folyamattal és a zaj következményeivel kapcsolatosak.

Mindenekelőtt tisztában kell lennünk azzal, hogy ez az elmélet az “információ” szót elég különleges módon használja; itt speciális értelme van, s egyebek között semmiképpen sem szabad összetéveszteni a jelentéssel. Meglepő, de igaz, hogy az itt alkalmazott szempontból két közlemény, amelyek közül az egyik igen gazdag jelentés, a másik pedig tökéletes értelmetlenség, az információ tekintetében teljesen egyenértékű lehet.

Ebben az új elméletben ugyanis az információ szó nem annyira arra vonatkozik, amit az ember csakugyan mond, hanem arra, amit mondhat. Vagyis az információ annak a mértéke, hogy mekkora a szabadságunk valamely közlemény kiválasztásában. Ha az ember abban az egészen elmei helyzetben van, hogy két alternatív közlemény között kell választani, önkényesen azt mondjuk, hogy az ehhez a szituációhoz tartozó információ egységnyi. Az információ fogalma (ellentétben a jelentés fogalmával) nem az egyedi közleményekre vonatkozik, hanem inkább a szituáció egészére, s egységnyi információn ekkor azt értjük, hogy az embernek ebben a szituációban olyan mennyiségű választási szabadsága van a közlemény megválasztásában, amelyet célszerű szabvány- vagy egységnyi mennyiségnek tekinteni. A két közlemény, amelyek között az embernek ilyen szelekció alkalmával választania kell, tetszés szerint bármi lehet. Lehet az egyik a Biblia szövege, a másik meg egy “igen”.

Az eddigiekben olyan mesterségesen egyszerű szituációkkal foglalkoztunk, amelyekben az információforrásnak csak néhány meghatározott közlemény között van szabad választása; olyan ez, mint amikor az embernek egyet kell kiválasztania egy véges számú születésnapi szabvány dísztávirat-sorozatból. Természetesebb és fontosabb az a szituáció, amelyben az információforrás az elemi szimbólumok halmazából sorozatosan választ, és az így kiválogatott szekvencia alkotja a közleményt. Így pl. az ember kiválaszthat egymás után több szót, s ezekből az egyedileg kiválogatott szavakból adódik a közlemény.

Nyilvánvaló, hogy a valószínűség igen nagy szerepet játszik a közlemény generálásában, s minden következő szimbólum megválasztása függ az előző választásoktól. Így pl. ha a legutoljára választott szimbólum az “a”, akkor nagyon csekély annak a valószínűsége, hogy a következő szó valamilyen névelő lesz vagy valamilyen igealak (kivéve az igenevet). E három szó után: “abban az esetben”, nagyon nagy annak a valószínűsége, hogy a következő szó “ha”, és nagyon csekély annak a valószínűsége, hogy a következő szó “elefánt”. Ugyanígy, kicsi a valószínűsége a következő szósorozatnak: “Konstantinápoly csúnya lazacot halászván”. Csekélynek csekély, de nem nulla; mert minden további nélkül elképzelhető egy olyan bekezdés, amelyben az egyik mondat azzal zárul, hogy “Konstantinápoly”, a következő pedig azzal kezdődik, hogy “Csúnya lazacot halászván”. (S hadd jegyezzük meg csak úgy mellesleg, hogy a szóban forgó szekvencia valóban előfordult egy kifogástalan mondatban, ti. a mi előbbi mondatunkban.)

Tény és való, Shannon kimutatta, hogy ha véletlenszerűen kiválasztott betűket vagy szavakat kizárólag valószínűségi megfontolások szerint szekvenciákba rendezünk, tendenciáját tekintve jelentéses szavakká és kifejezésekké szerveződnek.

Térjünk most vissza az információ gondolatához. Kiderül, hogy az a mennyiség, amely egyedül elégíti ki az információ mérésével szemben támasztott természetes követelményeket, pontosan azonos azzal, amit a termodinamikából entrópia néven ismerünk, s ami tulajdonképpen nem más, mint a véletlenszerűségnek, vagy ha úgy tetszik az “összevissza doboltságnak” a foka adott helyzetben. Ezt a mennyiséget a közrejátszó különféle valószínűségek terminusaiban fejezzük ki.

Akik foglalkoztak fizikával, azoknak igen sokatmondó az, hogy a kommunikációelméletben az információ mértékeként az entrópiára emlékeztető kifejezés jelenik meg. Az entrópia fogalma, amelyet Clausius német fizikus vezetett be majdnem száz esztendeje, szorosan kapcsolódik Boltzmann nevéhez, majd pedig Willard Gibbs (USA, Yale Egyetem) adott a fogalomnak mély értelmet a statisztikai mechanikáról szóló klasszikus művében. Ma már ez a fogalom annyira alapvető és elterjedt, hogy Eddington megállapította: “véleményem szerint az a törvény, amely szerint az entrópia állandóan nő – azaz a termodinamika második főtétele – a legelső helyet foglalja el a természettörvények között”.

Így, ha az ember a kommunikációelméletben találkozik az entrópia fogalmával, joggal fogja el az izgalom. Az, hogy az információ az entrópiával mérhető, végül is természetes, ha emlékezetünkbe idézzük, hogy a kommunikációelméletben az információ azzal függ össze, mennyi a választási szabadságunk a közlemények megszerkesztésében. Ezért egy kommunikációs forrásról ugyanúgy elmondhatjuk, mint ahogyan egy termodinamikai együttesről is elmondhatnánk; “ez a szituáció nagymértékben szervezett, nem jellemzi túlságosan nagy fokú véletlenszerűség vagy választási lehetőség, vagyis az információ, az entrópia, csekély”.

Szem előtt kell tartanunk azt, hogy a matematikai kommunikációelméletet nem az egyedi közlemények jelentése érdekli, hanem az információforrás statisztikai természete. Ezért nem meglepő az, hogy egy kommunikációs csatorna kapacitását az általa továbbítható információ mennyiségének terminusaiban írjuk le; helyesebben, a csatorna kapacitását aszerint kell leírni, hogy mennyire képes továbbítani azt, amit adott információforrás produkált.

A továbbító megteheti, hogy egy írásos közleményt valamilyen kód segítségével, mondjuk, számsorozattá rejtjelezzen, és azután ezek a számok haladnak át jelként [signal] a csatornán. Ezért általában véve azt mondjuk, hogy a továbbító funkciója a közlemény kódolása, a vevőé pedig ennek dekódolása. Az elmélet elképzelhetővé tesz rendkívül bonyolult továbbítókat és vevőket is, pl. olyanokat, amelyeknek “emlékezetük” van, s így az, hogy a közlemény valamelyik szimbólumát hogyan kódolják, nemcsak ettől az egy szimbólumtól, hanem a közlemény előző szimbólumaitól és azok kódolási módjától is függ.

Most már megfogalmazhatják a szóban forgó elmélet arra vonatkozó alapvető tételét, hogy milyen feltételekkel lehet diszkrét szimbólumokat továbbítani zajmentesen. A tétel olyan kommunikációs csatornára vonatkozik, amelynek kapacitása másodpercenként C egység, s amelybe másodpercenként H egységnyi jel érkezik az információforrásból. A tétel értelmében, ha megfelelő kódolási eljárásokat dolgozunk ki a továbbító számára, akkor lehetővé válik az, hogy a C/H arányt átlagosan megközelítő mennyiségben továbbítson szimbólumokat a csatornánk, mindamellett azonban – bármilyen szellemes legyen is a kódolás – ez a mennyiség sohasem haladhatja meg a C/H arányt.

Ha felületesen nézzük, pl. annak a durva analógiájára, ahogyan elektromos áramkörökben transzformátorokat alkalmaznak impedanciák kiegyenlítésére, merőben természetesnek látszik ez a tétel, amely szerint az a hatékony kódolás, amelyik összhangban van az információforrás és a csatorna statisztikai jellemzőivel. De ha az eredményeit alkalmazni képes rendkívül nagy számú helyzet közül bármelyikre nézve részletesen szemügyre vesszük, megértjük, milyen mélyreható és nagy kapacitású elmélettel van dolgunk.

Hogyan befolyásolja az információt a zaj? Az információ, amint erre szüntelenül emlékeztetnünk kell, annak a mértéke, hogy mekkora a választási szabadságunk egy közlemény kiválasztásában. Minél nagyobb ez a választási szabadság, annál nagyobb lesz annak a bizonytalansága, hogy a ténylegesen kiválasztott közlemény a megfelelő közlemény-e. Ilyenformán kéz a kézben jár a nagyobb választási szabadság, a nagyobb bizonytalanság és a nagyobb információ.

Ha bevezetjük a zajt, ez azt jelenti, hogy a vett közlemény tartalmaz bizonyos torzulásokat, bizonyos hibákat, bizonyos külsődleges anyagot, ami kétségtelenül növeli a bizonytalanságot. De ha megnőtt a bizonytalanság, az információ is megnőtt, és ez úgy hangzik, mintha a zajnak jótékony hatása volna!

Igaz, hogy ahol zaj van, a vett jel nagyobb sorozatból van kiválasztva, mint amelyet az adó szándékolt. Ez a szituáció nagyon szépen illusztrálja, milyen szemantikai csapdába eshet az ember, ha nem tartja mindig szem előtt azt, hogy itt az “információ” szót abban a különleges értelemben használjuk, miszerint a választás szabadságát, s ennél fogva a megejtett választás bizonytalanságát méri. Az adó választási szabadsága miatt keletkező bizonytalanság kívánatos bizonytalanság. A hibák miatt vagy a zajhatás miatt keletkező bizonytalanság viszont nem kívánatos bizonytalanság. A hibák miatt vagy a zajhatás miatt keletkező bizonytalanság viszont nem kívánatos bizonytalanság. Ahhoz, hogy megkapjuk a vett jelben a hasznos információt, le kell vonnunk belőle a hamis adagot. Ezt az elmélet azzal biztosítja, hogy bevezeti az “ekvivokáció” néven ismert mennyiséget. Ez a zaj által okozott kétértelműség mennyiségét jelenti. Ekkor, a zajmentes csatorna kapacitásának előbbi meghatározását finomítva vagy kiterjesztve, azt állítjuk, hogy a zajos csatorna kapacitása egyenlő az arány maximumával, amelynél hasznos információ (azaz a teljes bizonytalanság mínusz a zaj okozta bizonytalanság) továbbítható a csatornán át.

Végezetül megfogalmazhatjuk ennek az egész kommunikációelméletnek középponti tételét. Tegyük fel, hogy egy C kapacitású zajmentes csatorna információt vesz fel egy H entrópiaforrásból, amikor is az entrópia a forrásból érkező lehetséges közlemények számának felel meg. Ha a C csatornakapacitás nagyobb, mint H, vagy azzal egyenlő, akkor megfelelő kódolási rendszerek kidolgozása esetén a forrás kimenete tetszés szerinti kevés hibával továbbítható a csatornán át. Ha azonban a C csatornakapacitás kisebb, mint H, a forrás entrópiája, akkor lehetetlenség olyan kódokat kidolgozni, amelyek a hibagyakoriságot tetszés szerinti csekély mértékre csökkentik.

Bármily leleményes is a kódolási folyamat, a jel vétele után mindig marad bizonyos nem kívánatos bizonytalanság arra nézve, hogy mi volt a közlemény; és ez a nem kívánatos bizonytalanság – ez a zaj vagy ekvivokáció – mindig legalább annyi vagy nagyobb lesz, mint H = C. Mindig van azonban legalább egy olyan kód, amely ezt a nem kívánatos bizonytalanságot olyan értékre tudja mérsékelni, amely csak kevéssé haladja meg a H = C mennyiséget.

Ez az alaptétel pontosan és szinte lenyűgöző egyszerűséggel írja le, milyen az a maximális megbízhatóság, amely zaj jelenlétében működő kommunikációs csatornánál egyáltalán elérhető. Sokáig kell gondolkodnunk, és számos alkalmazást szemügyre vennünk, amíg teljesen felfogjuk azt, hogy ez a megdöbbentően tömör tétel valójában milyen alapvető és általános értékű. Egyetlen alkalmazást be is mutatunk itt, ehhez azonban egy pillanatra vissza kell nyúlnunk a valamely forrásból eredő információ gondolatához.

Miután kiszámítottuk egy bizonyos információforrás entrópiáját (vagy információját, vagy választási szabadságát), összehasonlíthatjuk ezt ennek az entrópiának a lehetséges maximális értékével, és csak azt a feltételt kell betartanunk, hogy a forrás továbbra is ugyanazokat a szimbólumokat használja. A tényleges és a maximális entrópia arányát a forrás viszonylagos entrópiájának nevezzük. Ha bizonyos forrás viszonylagos entrópiája – mondjuk – 0,8, ez nagyjából azt jelenti, hogy ez a forrás akkor, amikor megválasztja a szimbólumokat valamilyen közlemény megformálásához, kb. 80%-osan szabad ahhoz képest, amilyen ugyanezekkel a szimbólumokkal egyáltalán lehetne. Ha a viszonylagos entrópia értékét levonjuk egyből, az így kapott mennyiséget nevezzük “redundanciának”. Vagyis a közleménynek ez a része fölösleges abban az értelemben, hogy ha hiányoznék, a közlemény lényegileg akkor is teljes volna, vagy legalábbis kiegészíthető volna.

Mint érdekességet megemlítjük azt, hogy az angol nyelv redundanciája majdnem pontosan 50%. Más szavakkal: az írás vagy beszéd közben általunk megválasztott betűknek, illetve szavaknak kb. a fele szabad választásunktól függ, kb. a másik felét viszont tulajdonképpen a nyelv statisztikai struktúrája szabja meg, még ha ezzel rendszerint nem is vagyunk tisztában. Megemlítjük, hogy ez az 50% majdnem pontosan az a minimális szabadság (relatív entrópia), amely a betűk megválasztása terén szükséges ahhoz, hogy kielégítő keresztrejtvényeket lehessen szerkeszteni. Ha egy nyelvben csak 20%-os a szabadság, vagy 80%-os a redundancia, akkor lehetetlenség olyan bonyolultságú és olyan mennyiségű keresztrejtvényt szerkeszteni, hogy a játék népszerű lehessen.

Minthogy az angol nyelv 50%-ban redundáns, a távíró működéséhez szükséges időt kb. a felére lehetne csökkenteni megfelelő kódolással, feltéve, hogy zajmentes csatornában továbbítjuk az információt. Ha azonban a csatorna zajos, annak is van bizonyos reális előnye, mert akkor nem olyan kódolást alkalmazunk, amely minden redundanciát kiküszöböl. A megmaradó redundancia ugyanis segít a zaj kiküszöbölésében. Így pl. az angol nyelv nagy redundanciájának köszönhető az, hogy az ember a távirat kibetűzésekor könnyen ki tudja javítani a továbbítás folyamán keletkezett hibákat.

Mindeddig olyan kommunikációs rendszerekkel foglalkoztunk, amelyek csekély számú szimbólumból – mondjuk, betűkből – álló diszkrét sorozatok használatát tételezték fel. Feltételezhető, hogy az elmélet szinte összehasonlíthatatlanul bonyolultabbá válik akkor, ha folyamatos közleményekre akarjuk alkalmazni, olyanokra, mint amilyen pl. a beszédhang, amelynek magassága és energiája folytonosan váltakozik. Mint ez azonban oly gyakran történik, egy igen érdekes matematikai tétel siet a segítségünkre. Gyakorlatilag az embert mindig olyan folyamatos jel érdekli, amelynek alkotóelemei, az egyszerű harmóniák, esetenként nem az összes frekvenciát képviselik, hanem kizárólag azokat a frekvenciákat, amelyek a nulla frekvenciától – mondjuk – a W Hz frekvenciáig terjedő sávon belül helyezkednek el. Így, habár az emberi hang nagyobb frekvenciákat is tartalmaz, kielégítő kommunikáció biztosítható olyan telefoncsatornán, amely tegyük fel, csak 4000 Hz-ig terjedő frekvenciákat kezel. 10–12 000 Hz-ig terjedő frekvenciákkal megoldható a szimfonikus zene különlegesen hű rádióközvetítése.

Az említett tétel értelmében egy T másodperc időtartamú és 0-tól W-ig terjedő tartományon belül maradó frekvenciájú folyamatos jel tökéletesen leírható a 2 TW elemű számsorral. Ez csakugyan figyelemre méltó tétel. Általában véve egy folyamatos görbét csak megközelítően jellemezhetünk azzal, ha megadjuk valamilyen véges számú áthaladási pontját. Ha azonban a görbe korlátozott számú frekvencia szerint ingadozó egyszerű harmonikus alkotóelemekből épül fel, mint ahogyan egy összetett hang korlátozott számú tiszta hangzásból épül fel, akkor véges számú mennyiség teljesen elegendő a görbe hiánytalan meghatározásához.

Részint e tétel, részint a helyzet lényegi természete jóvoltából kiderül, hogy a folyamatos kommunikáció esetére kiterjesztett elmélet matematikailag valamivel nehezebb és bonyolultabb ugyan, de nem különbözik lényegesen a diszkrét szimbólumok elméletétől. A diszkrét esetre vonatkozó állítások jelentős részét nem is kell módosítani a folyamatos esetre, az állításoknak egy másik részét pedig csak csekély mértékben kell átalakítani.

A matematikai kommunikációelmélet annyira általános, hogy nem kell megmondani, milyen fajta szimbólumokról van szó, írott betűkről, vagy szavakról, vagy hangjegyekről, vagy kimondott szavakról, vagy szimfonikus zenéről, vagy festményekről. Az elmélet által feltárt összefüggések érvényesek mindezekre, de más kommunikációs formákra is. Az elmélet annyi képzelőerővel épült ki, hogy a kommunikációs probléma velejét ragadta meg.

Általános érvényének egyik bizonyítéka az, hogy jelentősen hozzájárul a titkosítás elméletéhez, amely természetesen nem más, mint a kódolás egyik formája; sőt, tulajdonképpen a titkosírás alapvető elmélete. Hasonlóképpen az elmélet hozzájárul az egyik nyelvről a másikra való fordítás problémáinak tisztázásához, habár itt a dolgok teljes megértéséhez az információn kívül nyilvánvalóan a jelentést is figyelembe kell venni. Továbbá, az ebben a munkában kifejtett gondolatok olyan szorosan kapcsolódnak a számítógépek logikai elrendezésének problémájához, hogy nem meglepő, ha Shannon tanulmányt írt arról, miként lehetne megtervezni egy jól sakkozó számítógépet. Közvetlenül függ össze mostani gondolatmenetünkkel ennek a tanulmánynak az a záró megjegyzése is, miszerint vagy azt kell mondanunk, hogy az ilyen számítógép “gondolkodik”, vagy pedig lényegesen módosítanunk kell a “gondolkodni” ige megszokott jelentéstartalmát.

Az elmélet továbbmegy. Habár látszólag csak a technikai szint problémáira alkalmazható, a szemantika és a hatékonyság szintjén is nagy segítséget nyújt, és gondolatokat ébreszt. Nagyon valószínű, hogy a kommunikációs rendszernek az 1. ábrán bemutatott formális diagramja kiterjeszthető úgy, hogy a jelentés és a hatékonyság legfontosabb problémáit is felölelje.

Így pl. ha átlépünk ezekre a szintekre, lényeges lehet a rendeltetési hely statisztikai jellemzőinek figyelembe vétele. Az ábra kiegészítéseként elképzelhetünk egy új blokkot, amelynek neve “szemantikus vevő”, s amely a jeleket közleményekké átalakító műszaki vevő és a rendeltetési hely között helyezkedik el. Ez a szemantikus vevő második dekódolásnak veti alá a közleményt, amelynek az a feladata, hogy biztosítsa a közlemény statisztikai-szemantikai jellemzőinek egyezését az összes elképzelhető vevőknek vagy a befolyásolni kívánt hallgatóságot képező vevőcsoportnak statisztikai-szemantikai kapacitásaival.

Elképzelhetünk még egy másik blokkot is az ábrán, amely az információforrás és a továbbító közé ékelődve a “szemantikus zajt” képviselné (és ez nem tévesztendő össze a “műszaki zajjal”). Ez képviselné azokat az információforrásból – mondjuk egy szónoktól – eredő jelentéstorzulásokat, amelyek nem szándékoltak, mégis elérik a rendeltetési helyet vagy a hallgatót. S a szemantikus dekódolás problémájánál feltétlenül figyelembe kell venni ezt a szemantikus zajt. Elképzelhető az eredeti közlemény olyan elrendezése is, hogy a közlemény összjelentése mínusz a szemantikus zaj egyenlő legyen a közleménynek azzal a teljes jelentésével, amelyet a forrás a rendeltetési hely tekintetében megkíván.

További mód, amellyel ez az elmélet elősegítheti a kommunikáció tökéletesítését, azzal a ténnyel függ össze, hogy bármennyire jó a kódolás, a hibamennyiség és a zavar csak nő, a vétel hűsége pedig csökken, ha túl sokat akarunk bezsúfolni a csatornába. A valamennyi szintre vonatkozó, általános érvényű elméletnek a csatornakapacitáson kívül nyilván figyelembe kell vennie (még a szavak is helytállóak!) a hallgatóság kapacitását is. Ha az ember túlságosan igénybe veszi a hallgatóság kapacitását, valószínűleg nem az történik – közvetlen analógiával élve –, hogy jól feltöltjük a hallgatóságot, és a felesleg legfeljebb kifolyik. Sokkal valószínűbb az – megint csak közvetlen analógiával –, hogy általános hibatömeget és zűrzavart idézünk elő.

Az elmélet által kidolgozott információfogalom első pillantásra csalódást kelt és bizarrnak látszik. Csalódást kelt, mert semmi köze a jelentéshez, és bizarr, mert nem az egyedi közleményre vonatkozik, hanem közlemények valamely átfogó együttesének statisztikai jellegére, továbbá bizarr azért is, mert ebben a statisztikai értelemben az információ és a bizonytalanság szó kéz a kézben jár. Az alaposabb vizsgálódás azonban megmutatta, hogy ez az elemzés annyira megtisztította a levegőt, hogy talán most van első ízben lehetőségünk valódi jelentéselmélet kidolgozására. A műszaki kommunikációelmélet pontosan olyan, mint egy tökéletesen megbízható és diszkrét leány, aki a postán felveszi a táviratomat. Ügyet sem vet a távirat jelentésére, legyen az szomorú, vidám vagy zavarba ejtő. Ellenben késznek kell lennie arra, hogy intelligensen kezeljen minden közleményt, amely csak az asztalára kerül. Az a gondolat, hogy a kommunikációs rendszernek igyekeznie kell megfelelően kezelni minden lehetséges közleményt, és hogy ennek intelligens módja az, ha a rendszer elrendezését a forrás statisztikai jellegére alapozzuk, kétségkívül általánosságban is jelentős a kommunikációt illetően. A nyelvet úgy kell megtervezni, illetve fejleszteni, hogy a szemünk előtt lebegjen mindannak a totalitása, amit az ember csak mondani óhajthat; de még ha nem is biztosíthat mindent minden esetben, akkor is a lehető leggyakrabban, a lehető legjobban kell elvégeznie feladatát. Azaz szintén statisztikailag kell megközelítenie a feladatot.

Tanulmányunkban példa gyanánt tényeket közöltünk az angol nyelv statisztikai struktúráját illetően. Ezek a nyelv és a kommunikáció bármelyik fázisának kutatói számára nyilvánvalóan fontosak. Különösen ígéretesnek látszik az a javaslat, hogy a valószínűségelméletet alkalmazzák a szemantikai kutatásban. Leginkább használhatónak látszik a valószínűségszámításnak az a nagy kapacitású fejezete, amely a matematikusok által Markov-folyamatoknak nevezett területtel foglalkozik, s amelynek értelmében a múltbeli események befolyásolják a jelenbeli valószínűséget. Ez az elmélet ugyanis különösen alkalmas arra, hogy megragadja a jelentés egyik legfontosabb, de egyben legnehezebb aspektusát, nevezetesen a szövegösszefüggés befolyását. Az emberben az a homályos érzés keletkezik, hogy az információról és a jelentésről kiderülhet, hasonlítanak a kvantumelméletből ismert valamelyik kanonikusan összekapcsolt változópárhoz, amennyiben olyan természetű közös korlátozásnak vannak alávetve, hogy fel kell áldozni valamennyit az egyikből, ha többet akarunk a másikból. Vagy esetleg kiderülhet a jelentésről, hogy analóg az egyik olyan mennyiséggel, amelyektől a termodinamikai együttes entrópiája függ. Ezzel kapcsolatban Eddingtonnak van egy igen ideillő megjegyzése:

“Tegyük fel, felkérnek minket arra, hogy rendezzük el két kategóriában a következő fogalmakat: távolság, tömeg, elektromos energia, entrópia, szépség, dallam.

Azt hiszem, nyomós okok szólnak amellett, hogy az entrópiát a szépség és a dallam mellé, ne pedig az első három fogalom mellé soroljuk. Az entrópiát csak akkor fedezzük fel, ha a részeket kapcsolódásukban szemléljük, s a szépséget és a dallamot éppen azáltal észleljük, hogy a részeket kapcsolódásukban látjuk, illetve halljuk. Mind a három fogalom elrendezése vonatkozik. Átütő gondolat, hogy e három társfogalom közül az egyik képes arra, hogy a természettudomány közhelyszámba menő mennyiségeként szolgáljon. Annak, hogy ez az idegen oly biztonságosan tud eligazodni a fizikai világ bennszülöttei között, az a magyarázata, hogy beszéli a nyelvüket, vagyis az aritmetika nyelvét.”

Bizonyosan érzem, hogy Eddington a jelentés szót is hajlandó lett volna a szépség és a dallam mellé helyezni; s azt gyanítom, örömteli izgalommal fedezte volna fel az itt tárgyalt elméletben, hogy az entrópia nemcsak az aritmetika nyelvét, hanem a természetes nyelvet is beszéli.