KOMMUNIKÁCIÓ, KÖZVÉLEMÉNY, MÉDIA
2014/2. szám
|
KOMMUNIKÁCIÓ, KÖZVÉLEMÉNY, MÉDIA 2014/2. szám |
DOI: 10.20520/Jel-Kep.2014.2.4
Az alábbi tanulmány egy problémafelvetés is. Azt kívánja megmutatni, hogy a - kétségtelenül fiatal - kommunikációtudományok számára lehetséges, és alighanem szükséges is az olyan tudományoknak a tanulmányozása, mint amilyen a fizika. A megfontolás - és szükség esetén a hivatkozás is - akár ugyanaz lehet, mint a filozófiáé, amely az emberi megismerés lehetőségeit kutatja, például az eszmetörténet keretében. Ez utóbbi esetben a kutatások során a gondolkodás feltárása kerül középpontba, ehhez képest specifikus perspektívákat adhatnak a kommunikációs elméletek: lehetséges a tudományos rendszerek és változásaik elemzése olyan fogalmakon alapuló rendszerek szempontjából, mint az információ, az interakció, a tudás-kultiváció, a tudományos közösségek hálózata, a jelentések stb. És ugyanazon okokból, mint a filozófia esetében, kiemelt jelentőségű lehet a fizikai rendszerek értelmezése (ezek részletezését azonban itt most nem tekintem célnak).
E tanulmány a fizikai elméleti rendszereket nyelvi rendszerekként definiálja, és ezek egymáshoz való viszonyulásait és ezek következményeit vizsgálja. Vagyis az elgondolás szerint ezek a rendszerek nem következnek egymásból, nem valamilyen egyenes vonalú fejlődés vonalán nőnek ki egymásból, hanem olyan zárt rendszerek, amelyek között fordítási viszonyokat lehet megállapítani. A fordítási viszonyok esetenkénti kialakulása sajátos helyzetet eredményez, és ez nem vezethető le az adott elméleti-nyelvi rendszerekből. Olyan valódi történés eredménye e helyzet, amelyet a kommunikációelméleti aktus fogalmából értelmezhetünk. Tanulmányom tehát a nyelvi (szignifikációs) rendszer, a fordítási viszony és az aktus fogalmainak perspektívájából tekint az elemzés tárgyára.
Ezzel egy lehetséges interdiszciplináris területet és kutatási programot fogok vázolni. Az elemzés tekintettel próbál lenni arra, hogy mind a kommunikációtudomány, mind a fizika sajátos kérdései és megközelítései értelmezhetők legyenek a másik perspektívájában. Ezért többször éltem a leegyszerűsítés eszközével, jó néhányszor támaszkodtam az egyes fogalmak köznyelvi jelentésére vagy az ezekhez kapcsolódó asszociációkra. Mindazonáltal a tanulmány utolsó harmadában e fogalmak egy lehetséges elméleti kategorizálását is bemutatom.
Mindenekelőtt mindjárt az elején három példán szemléltetem azokat a fizikatörténeti fordulatokat és problémákat, amelyeket a fenti fogalmak sajátosan világíthatnak meg. Ezt követően e fogalmak értelmét, perspektíváit rajzolom meg. Majd kitérek arra a kérdésre, amely a természettudományi és társadalomtudományi elméletalkotási módok közötti különbséget illeti, előbbi mint a leírás tárgya, utóbbi mint a leírás eszköze érdekes. Ezután pedig a fenti fogalmak kommunikációelméleti perspektívájából azokat a kérdéseket vizsgálom meg, amelyek a fizikai elméletek nyelvi rendszerekként való értelmezéséből válnak láthatóvá, felvethetővé. Végül egy konkrét elmélet, a kommunikáció participációs elmélete keretében egy konkrét alkalmazási lehetőséget is bemutatok.
Az első választott példa a buborékkamrát írja le. Ez egy olyan kísérleti eszköz, amelyben atomi vagy szubatomi részecskék tanulmányozása történik. Ezeket a részecskéket nagy energiával és sebességgel ütköztetik, ennek eredményeként apró "robbanások", újabb részecskék jönnek létre, és különböző irányokba, különböző pályákon szétszóródnak. A buborékkamra ezeket az eseményeket teszi láthatóvá például úgy, hogy a kamrába bevezetett speciális ködben ezek különböző formájú kicsapódásokat okoznak. A fizikusok a rajzolatoknak az elemzésével következtetnek a lezajlott folyamatokra, részecskékre és tulajdonságaikra. A példában azt kell látni, hogy a megfigyelők valójában nem a megfigyelni kívánt jelenségeket figyelik meg, hanem ezek áttételét. Azok ugyanis nem az emberi tapasztalás világában vannak, át kell vezetni egy olyan világba, ahol a sajátos biológiai organizmusok érzékszervei és érzékelési sémái működnek.
Felületesen szemlélve egy technikai jellegű megoldást látunk, ahol egy az elemi részecskék elmélete alapján kialakított kísérleti berendezésben zajló folyamatok vizsgálatára egy erre alkalmas megfigyelő berendezés kapcsolódik. A megfigyelés és eszközének működése látszólag alárendelt a megfigyelendő jelenségeket kiváltó berendezésnek. A két berendezés valójában két elméleti rendszer alapján került kialakításra. A megfigyelést lehetővé tevő berendezés szükségszerűen olyan fizikán alapul, amely az emberi érzékeléshez kapcsolódik, az emberi léptékekhez mérhető makroszintű folyamatok előállítását szolgálja. Ez legkézenfekvőbben klasszikus fizikát jelent, klasszikus természeti törvényekkel. A megfigyelni kívánt jelenségeket előállító berendezés azonban egy másféle fizikát feltételez, emberi léptékkel nem mérhető mikroszintű folyamatokkal. Ez nem klasszikus fizika, olyan természeti törvényekkel, amelyek egészen más jellegűek mint a klasszikusak. Különböző nyelvi rendszerekről beszélhetünk tehát, elkülönültségükből pedig az következik, hogy fordítási viszony lehet közöttük. Bár matematikailag lehetséges közös elemeket találni e rendszerekben, így lehetséges egy közös keretet feltételezni, és lehetséges ezeket a matematikai "folyosókat" a fizikai világban ok-okozati összefüggésként értelmezni, ez jelen tudásunk szerint a kvantummechanika megjelenése óta igencsak problémás (egyes megfogalmazásokban a mikro- és makroszintű világok között a természeti törvények - mint amilyenek az ok-okozati összefüggések is - összeomlanak).
A második példa vonatkozzon a gravitációs elméletre. A Kopernikusz, Kepler, Galilei és Newton nevéhez kötődő elméleti rendszer megalkotása és végső formába öntése egyfajta természetes fejlődési folyamatként jelenik meg több tudomány- és elmélettörténeti szövegben. Néhány megfigyelés, heurisztikus felismerés, fogalmi meghatározás és levezetés kézenfekvően vezetett el a kiteljesedett elmélethez. Kopernikusz megmutatta, hogy a Földről megfigyelt bolygók bonyolult mozgása teljesen érthetővé és egyszerűvé válik, ha Nap körüli körpályákhoz rendeljük ezeket. Kepler némi pontosítással, körök helyett ellipszis pályákra rajzolva őket, az ellipszis tulajdonságaival adta meg a mozgásaik szabályait. Felismerte, hogy a Naptól távolodva lassuló és közeledéssel gyorsuló bolygók a bejárt ellipszisen mindig egységnyi idő alatt ugyanakkora területet "sepernek" végig. Galilei a földi körülmények között található tárgyak mozgási törvényeit határozta meg, felismerve a tömeggel bíró testek tehetetlenségét, azt, hogy ezek a testek egyenes vonalon és egyenletesen haladnak tovább a rájuk ható külső erő megszűntével. Newton pedig a gravitáció hatására mozgó objektumok leírását általánosította, magában foglalva így mind a földi, mind az égi, tömeggel rendelkező objektumok előbbi mozgástörvényeit.
Ebben az elméletben azonban két igen különböző világ kapcsolódik össze: a bolygók mozgásait meghatározó geometriai összefüggések és a földi körülmények között mozgó tárgyak törvényszerűségeit összefoglaló mechanika rendszerei. Hogy ezek egymásnak való megfeleltetése mennyire nem magától értetetődő, a kulturális kontextusukban még inkább megmutatkozik: a földöntúli égi szférák tökéletes harmóniái és a földi árnyékvilág esetlegességektől és tisztátalanságoktól sem mentes anyagi világok kerülnek közös nevezőre. A két világ közötti átjárhatóságot, a két világra vonatkozó értelmezési rendszerek közötti "fordítás" lehetőségét leginkább a vallási és misztikus világképek fogalmazták meg korábban. Newton ezt gondolta tovább, feltételezte, hogy a mennyei égi törvényeknek valamilyen tükröződésük, jeleik kell legyenek az isten képmására teremtett ember számára ebben a világban. A fordítás eredménye az lett, hogy ugyanazon matematikai formájú erő és kölcsönhatás összefüggésekkel lehetett ekvivalenssé tenni az égi objektumok geometriáját és a földi objektumok mozgástörvényeit. A két világ nemcsak összeért, hanem egységesnek mutatkozott, ez aztán alapjaiban borította fel a két világ dichotómiájának világképét. A modern természeti törvény fogalma ezzel az általánosítással született meg.
A harmadik példa legyen egy elméleti probléma, amely bizonyos megfigyelések összeegyeztethetetlenségét mutatja. A fizika történetében jól kialakult helye van az objektumokkal és a hullámokkal foglalkozó elméleteknek. Ezek látszólag különböző tulajdonságokat vizsgálnak, az objektumok nem viselkednek hullámként, a hullámok pedig nem anyagi típusú dolgok. A szubatomi szinteken végzett kísérletek azonban zavarbaejtő eredményeket mutatnak. Például olyan tömeggel bíró részecskék, mint amilyen az elektronok is, egyes kísérletekben objektumként, korpuszkulaként viselkednek, másokban pedig hullámként. A kétféle viselkedés azonban nem egyesíthető egyetlen megfigyelési aktusban: például egy ablakon áthaladva az elektron-korpuszkulák csak a keret által kijelölt egyenes vonalú pályán haladnak (ahogyan egy elhajított labda, amely nem tud eltalálni, ha nem állunk az ablakban), az elektron-hullámok pedig a keret mögé is behatolnak (ahogyan a hanghullámok, amelyek akkor is elérnek hozzánk, ha nem állunk az ablakban)[1]. Ez ellentmondás.
Hogy melyik arcukat mutatják az elektronok, az egyik vagy másik elméletnek megfelelő kísérleti és megfigyelési helyzettől függ - a megfigyelő elkerülhetetlenül kijelöli a lehetséges viselkedési módot, így beavatkozik a megfigyelés tárgyába. E paradoxonnak a magyarázatára jött létre a kvantummechanika, a paradoxont azonban lényegileg nem sikerült feloldani, mi több, éppen erre az összegyeztethetetlenségre épült. És nincsen egyértelmű értelmezés arra nézve, hogy a paradoxon hol keletkezik: a világban található dolgok viselkedésében, a megfigyelésben vagy pedig az elméletalkotás módjában. Fordítási helyzetről beszélhetünk tehát, hiszen kívánatos a két elmélet és alkalmazásaik egymásnak megfeleltetése, fordítási problémaként értékelhető azonban, hogy matematikailag sem képezhető le egyik összefüggésrendszer a másikra. Az egyesítő elmélet pedig olyan elvre épül, amely ezekre egyszerre lehetségesként tekint.
A példák, amelyek sorát lehetne bővíteni, alapvető kérdéseket vetnek fel a fizikában is. Kommunikációs szempontból az lehet figyelemre méltó, hogy ezeket az "eseteket" minden különbözőségük ellenére fordítási problémaként lehet azonosítani. A fordítások kimenetele valódi - tudománytörténetiként értékelhető - történések (minden problematikusságuk mellett), és talán érdemes azokkal az értelmezési szempontokkal közelíteni, amelyeket a kommunikációs fogalomtárból vett aktus fogalma kínál.
A fordítás fogalma azt fejezi ki, hogy a nyelvi elemek nem önmagukban léteznek, hanem bizonyos rendszerekbe ágyazódnak, "megértésük" egy másik rendszerben sajátos műveleteket kíván. Átemelésük változásokat hoz létre az adott nyelvi elemeken, e változások a befogadó rendszertől függenek. Új összefüggések részei lesznek, új jelentést kapnak (még akkor is, ha a befogadó rendszer igyekszik a kibocsátó rendszerben lehetséges értelmüket visszaadni), használati módjaik az új rendszernek fognak megfelelni. Az átvételek következményeként azonban a befogadó rendszer maga is megváltozhat.
A nyelvi aktus fogalma azt fejezi ki, hogy a nyelvi konstrukciók nem csupán reprezentálnak bizonyos tartalmakat bizonyos szabályok teljesítésével, hanem használatuk esemény jellegű. Úgy hoznak létre bizonyos nyelvi helyzeteket, hogy azok az adott nyelvi megnyilvánulás előtt nem álltak fenn.
E két fogalom talán heurisztikus kiindulópont lehet a fizikai elméletek esetében is. A nyelvi aktus fogalma például azt mutatná meg, hogy a fizikai elméletek nem csupán tükröző leírásai a világnak, hanem minden egyes reprezentáció új helyzetet hoz létre egy elméleten belül, esemény jellegű. A fordítás fogalma azt lenne képes megmutatni, hogy a fizika különböző elméleti rendszereinek fogalmai e zárt rendszereken belül meghatározottak, átvitelük más elméleti összefüggésekbe változást hoz létre e fogalmakon, de a befogadó rendszerekben is.
Kérdés azonban, hogy a természettudományok (köztük a fizika) és a társadalomtudományok (köztük a kommunikációtudományok) logikái különböznek-e, különböző célokat tűznek-e ki, és vizsgálati módszereikkel különbözőképpen tekintenek-e a tárgyukra? Kérdés ugyanis, hogy ez utóbbi összefüggésrendszerből származó fogalmak - így a nyelvi aktus és a fordítás fogalmai - alkalmazhatók-e az előbbi rendszereken?
A legáltalánosabban, mondhatni szlogenszerűen, azt a különbséget szokták emlegetni, ami az "objektív" és a "szubjektív" megközelítésmód meghatározó voltát illeti egyik és másik esetben. E két jellemzés problematikájával e helyütt nem kívánok foglalkozni, nagy irodalma van a filozófiában, de például a módszertani elemzésekben, a pszichológiában, a szociológiában stb. is. E különbség tekintetében itt csak néhány alapvető sajátosságot emelnék ki.
A természettudományok - és kiváltképpen a fizika - egy a megismerőtől független valóságra irányul. Eredményeit olyan formában írja le, hogy azok függetlenek a megismerést kivitelezőtől és eszközeitől, és olyan törvényeket rögzít, amelyek a leírandó univerzum egészében érvényesek (így bárhol megfigyelhetők). A társadalomtudományok, így a kommunikációtudományok is, ezzel szemben olyan valóságra irányulnak, amely nem független a megismerőtől, hiszen a megismerő a viselkedésmintáival, a gondolkodásával, a nyelvével része a leírandó társadalmi világnak. A leírás eredményei függnek a leíró egyéni és egyedi megközelítésétől, eszközeitől, értelmezéseitől, gondolkodásmódjától és a leírás kontextusától. Ezektől nemcsak hogy nem lehet elvonatkoztatni, hanem éppen ezek feltárása lehet a feladat.
A leírások formáját tekintve a legszembetűnőbb különbség a formalizmusok használatában mutatkozik meg. A természettudományok jellemzően matematikai apparátusokat dolgoznak ki, ezek hiánya a modern természettudományokban egyenértékű a megalapozatlansággal. A társadalomtudományok viszont jellemzően kerülik a formalizmusokat, az ezekre való redukció a modern társadalomtudományokban egyenértékű a társadalom, különösképpen az emberi mivolt félreértésével. Természetesen ez a különbség nem szükségszerű és nem is teljesen általános. Ellenpéldákat találunk mindkét oldalon és mindegyiknek megvan a maga értelme: például a természeti törvényekre vonatkozó szemlélet és elvek megfogalmazása az első esetben, a logikai összefüggésekre és következtetésekre való hivatkozás a második esetben.
A formalizmusokhoz való viszonyulás a két tudományág esetében sajátos funkcióval bír. A formális rendszereknek a legfontosabb tulajdonságuk az, hogy a bennük szereplő elemeknek és összefüggéseknek nincsen jelentésük, nem vonatkoznak a rendszeren kívüli valóságra. Az összefüggések igazolása kizárólagosan a rendszerben adott feltételek alapján történik, az elemek pedig ezekben az összefüggésekben nyerik el értelmüket; így ezek a rendszerek ideálisan teljes mértékben zártak. A természettudományok az ilyen típusú rendszerekben való reprezentációval garantálják a megfigyelőhöz és az értelmezés partikularitásához kapcsolódó szubjektivitástól való elvonatkoztatást. Ezekben a rendszerekben ugyanis meghatározhatók az általános érvényességeket biztosító szabályok anélkül, hogy a nem általánost - a megfigyelési helyzetre jellemző partikularitást - definiálni kellene. A társadalomtudományok ellenben e zárt rendszerekre való leképezésekben éppen az egyedi kontextusok megszüntetését, a racionális értelmezések partikuláris kulturális adottságaitól való megfosztását látják. Mindezek ellenére sem a természettudományok nem nélkülözhetik a jelentésnélküli zárt rendszerek visszacsatolását a rendszeren kívüli világhoz, sem a társadalomtudományok nem tekinthetnek el a logikai igazolhatóságtól, ami viszont zárt rendszert feltételez. Mindkét tudományterületet a maga feloldhatatlan paradoxona hajtja.
A két tudományág látszólagos távolódása e két fókusz erősödésében érzékelhető. A természettudományokban a formális kalkulusok segítségével egyre elvontabb és az emberi tapasztalati világ számára egyre leképezhetetlenebb elméletek jönnek létre, a társadalomtudományok jelentős részében pedig a diskurzivitás megelőzi a formálisan-logikailag reprezentálható következmény-analízist, a társadalmi konstrukció az igazolást. A modern tudományok világképei, önértelmezései és módszertanai azonban nem a hasonulás irányába mutatnak. Meghatározóvá válik bennük előbbi esetben a társadalmi hátterek formális dekontextualizálása, illetőleg a második esetben a diskurzív kontextualizálás ereje, sajátos irányultsága, intencionalitása. A távolódás bizonyos szempontból nem meglepő: a modern társadalmakat általában is a társadalmi alrendszerek differenciálódása jellemzi.
A korábban vázolt három példában, bár a fordítás intuitív fogalmában kerültek összehasonlításra, valójában a fogalmat két síkra kell helyezni. E két síkot a fizika első- és másodrendű kérdéseinek tartományaként kommunikációs szempontból szükséges megkülönböztetni.
Az első síkon lehetséges feltételezni, hogy a világ olyan természeti törvények szerint rendezett, amelyek nyelvi - például logikai - strukturáltságot mutatnak. Lényegében nem is tudunk másféle világot feltételezni. Olyat nem, amelyik nem strukturált vagy éppenséggel "nem logikus" felépítésű és működésmódú (például ellentmondásokat enged meg). Ebben az esetben ugyanis ki kellene zárni a megértés lehetőségét, amennyiben azt gondoljuk, hogy a megértés valamilyen logikai-nyelvi elrendezést jelent. Előbbi feltételezéssel a fizikai leírásokat egyfajta, a természet nyelvének "olvasataként" kellene kivitelezhetőnek látnunk. Ez minden bizonnyal egy egységes fizikai elméletet kellene eredményezzen, ha feltételezzük, hogy maga a világ is egységes a természeti törvények általános jellegéből fakadóan. Mégis inkább fordításként kell látnunk a világ és a leírások viszonyát, amikor azt tapasztaljuk, hogy a sokféle és egymástól különböző leírások - fizikai elméletek - nem valamilyen egység részei, hanem önmagukban értelmezhetők, teljesek, és valódi probléma ezek összekapcsolása. Mi több ezek az egyesítési kísérletek valójában újabb specifikus részelméleteket eredményeznek, amelyek ismét csak összeolvasztásra várnak.
A fordítások második síkja éppen az elméleti rendszerek, mint nyelvi rendszerek viszonyát tartalmazza. Míg az első síkon az a kérdés, hogy a nyelven, elméleti rendszeren túli világ hogyan érthető meg ezekben, a második síkon az a kérdés, hogy ezek a nyelvi, elméleti rendszerek milyen kapacitásokkal bírnak, milyen leírásokat tesznek lehetővé, és hogyan viszonyulnak egymáshoz. Azt gondolom, hogy valójában az első síkbeli - "első vonalbeli" - kérdésekre e második síkbeli kérdésekkel is kereshetők bizonyos válaszok. Így a második síkon kommunikációs problémákként vizsgálhatók a nyelviként értelmezett elméleti rendszerek által felvetett kérdések. Az első síkon, a tényekre irányuló és az elméletek erre vonatkozó verifikációjával kapcsolatos kérdések feltételére leginkább a filozófiának sikerült perspektívát adnia. A második síkon néhány olyan alapvető, a fizikai elméletekre jellemező meghatározó állapítható meg, amely az itteni elgondolás szempontjából fontos lesz.
Elméleteknek minősülnek azok a nyelvi rendszerek, amelyek természeti törvényeket írnak le. Természeti törvénynek olyan összefüggések minősülnek, amelyek általánosak (például a gravitáció törvénye akkor minősül törvénynek, amennyiben állítható, hogy a tömegeket és a tömegközéppontok közötti távolságokat tartalmazó képlet a világban mindenhol érvényes). Nem értelmezhető az adott elmélet szempontjából a világon olyan hely, ahova ez az általánosság nem terjed ki, kivonja magát az elméletet meghatározó törvény hatálya alól. A világ "világságát" ugyanis a természeti törvények "rendje" határozza meg. Az adott elmélet szempontjából nem képzelhető el e "világon túli" világ, vagy "nem-világ". De még egy olyan határsáv sem, ahol a törvény hatálya fokozatosan gyengül és megszűnik, ugyanis a kicsit tövény, a "kevésbé-törvény" már nem törvény (hangsúlyozom azonban, hogy például nem arról van szó, hogy a világűrben a nagy objektumoktól távolodva a gravitációs erő ne gyengülhetne, hanem hogy a gravitációs vonzás erősségét meghatározó törvény "gyengülése" az, ami elképzelhetetlen). Lényegében ugyanez áll a természeti törvények keveredésére is: azok a törvények, amelyek nem különíthetők el, így nem reprezentálhatók expliciten (például matematikai formulákkal), nem minősülnek természeti törvénynek. Ha azt képzeljük, hogy az egyes természeti törvények különböző helyeken különböző formákat ölthetenek más törvényekkel való keveredésükben, akkor nem értelmezhető az általánosságuk (nem arról van szó, hogy például egy mágnes közelében mozgó testre kevésbé hat a gravitációs törvény, hogy a mágnesességet leíró törvény gyengíti a gravitációs törvényt, keveredik vele, hanem arról van szó, hogy a két törvény önmagában érvényes, a végső mozgást pedig a két független törvény hatásának az összegződése adja).
Három tulajdonságát állapíthatjuk meg tehát a természeti törvények fogalmán alapuló elméleti rendszereknek: teljesek, mert a törvények általánossága meghatározza a világ fogalmát, zártak, mert a világ fogalmának érvényessége nem terjeszthető ki az általánosan megfogalmazott természeti törvényeken túl (a "nem-világra" vagy homályos határsávra), és a természeti törvények önmagukban érvényesek, függetlenek (nem keverednek).
Innen már jól látszik a probléma: amennyiben egy elmélet független összefüggéseken alapulva teljes, zárt, hogyan lehetséges, hogy más elméletek viszonylatában, amelyek szintén teljesítik e kritériumokat, mégis csupán alternatívák, így "partikulárisak"? Ha önmagukban teljesítik is e feltételeket (belső perspektívában), egymás közötti viszonyukban (külső perspektívában) valójában ezek nem teljesek, nem zártak, a természeti törvények nem önmagukban érvényesek? Tisztán fizikai szempontból nehéz a kérdést megközelíteni, és valahogy így lehet megfogalmazni: milyen vonatkozásaik vannak a természeti törvényeknek érvényességük határain túl, például egy másik elméletben, vagy a két elmélet összekapcsolásában? Más megfogalmazásban: ha a természeti törvény fenti tulajdonságain alapuló nyelvi rendszer zárt, hogyan nyitható ki, hogy más zárt rendszer(ek)hez kapcsolódjon? A probléma paradoxonát minden elméleti fizikus ismeri. A leggyakrabban megfogalmazható válasz az, hogy találni kell egy olyan absztraktabb és általánosabb fogalmat vagy törvényt, amely magában foglalja az összekapcsolni kívánt elméletek törvényeit, így ezek specifikus vagy lokális megnyilvánulásokként értelmezhetők. Láttuk azonban fentebb, hogy az ilyen fogalmakon alapuló elméletekből is többféle alternatíva állhat elő, így a kérdések nem oldódtak meg.
A fordítás fogalmának az az értelme, hogy az összekapcsolni kívánt nyelvi rendszereket meghagyja zártságukban, nem igényli ezek megnyitását, fogalmaiknak, összefüggéseiknek összekeverését vagy gyengítését. A fordítás fogalma akkor működik, ha a fordítást végző nyelvi rendszerben a jelentések - a benne található fogalmak és összefüggések jelentései - adottak, rögzítettek, illetőleg a fordítandóra is úgy tud tekinteni, hogy a jelentések - a fordítandó fogalmak és összefüggések jelentései - adottak, rögzítettek. A fordítás fogalma tehát a problémát az egyes nyelvi rendszerek által meghatározott jelentések dimenziójába tereli.
Azt állíthatjuk, hogy a természeti törvény jelentése akkor adható meg, ha megfelel a fentebb felsorolt kritériumoknak. A fordítás fogalma az elméleti-nyelvi rendszerek zártságának meghagyásával tulajdonképpen a fordítás szempontjából alapvető fontosságú jelentéseket (a természeti törvényekét) hagyja meg, vagy még inkább ezeknek a jelentéseknek az adottságát feltételezi. A kérdés ezután az: mi lesz a fordításoknak az eredménye, következménye?
Kommunikációelméleti szempontból a fordítás megtörténte itt "erős" műveletnek számít. Ugyanis olyan jelentések kerülnek kapcsolatba vagy vannak hatással egymásra, amelyek korábban nem érintkeztek. A fordításnak olyan következményei lehetnek, amelyek e művelet előtt nem voltak lehetségesek, nem voltak "számításba véve". Ez a kép megfelel a (nyelvi) aktus korábban vázolt fogalmának. A nyelvi aktusok nem csupán nyelvi műveletek - egy nyelv valamely műveleti szabályának végrehajtásai, egy nyelv belső perspektíváját meghatározó feltételek közötti eljárások -, hanem események, amelyek a nyelven kívüli világban mennek végbe, a nyelv külső perspektívájában fejtik ki hatásukat.
Ezt a megállapítást lehet összekapcsolni a fordítás fogalmával. A fordítások szintúgy külső perspektívában jönnek létre - a nyelvi rendszerek közötti "térben" -, bár az eredmény a fordítást végző nyelv belső perspektívájában lesz láthatóvá valaminek a "beemelésével", értelmezésével. Mind a fordítás, mind a nyelvi aktus esetében egy nyelvi rendszer belső perspektívájában értelmezett valami, ami a nyelvi rendszer külső perspektívájában végbement eseményhez kapcsolódik. A fizika másodrendű kérdéseinek síkján tehát e két fogalom szemléletes képet rajzolhat. Vetítsük a korábbi három példára ezeket a kérdéseket.
A három példában olyan elméletpárokat és ezeknek megfelelő megfigyelési helyzeteket állítottunk egymás mellé, amelyek elkülönültek egymástól. Az elméleti rendszerek úgy fogalmaztak meg természeti törvényeket, hogy ezek függetlenek, összefüggésrendszereik teljesek és zártak voltak. A törvény jellegű összefüggések függetlenségét leginkább a matematikai kifejezések formalizmusa tükrözi. Az ezeken alapuló rendszerek teljessége abban mutatkozik meg, hogy összefüggéseik nem igénylik a másikhoz való kapcsolást, viszonyítást, kiegészítést. Zártságuk abban nyilvánul meg, hogy a természeti törvények hatóköre nem terjeszthető ki a másik rendszerre. Ez az elméletek belső perspektívája, a természeti törvények itt értelmezhetők e kritériumokkal.
A buborékkamra esetében a mikrofizika és makrofizika rendszerei nemcsak matematikájukban teljesek és zártak, hanem a megfigyelhető jelenségek kijelölésében is: egyik esetben atomi vagy szubatomi részecskékre és tulajdonságaikra, másik esetben a kicsapódások fizikai tulajdonságaira vonatkoznak. Egyik rendszerben leírható tulajdonságoknak sem kell a másikban megadható tulajdonságokra hivatkoznia, sőt ezek összekapcsolása bizonyos értelemben esetleges.
A Kepler és Galilei-féle világok is különböző matematikai - geometriai, illetve mechanikai összefüggéseket tartalmazó - rendszerekben fejeződnek ki, amelyek formális reprezentációikban nem kapcsolódnak. A megfigyelhető jelenségek tekintetében az előbbi példához hasonlatosak, az égi terek és a földi világ úgy viszonyultak egymáshoz, mint a makro- és mikrovilág. Elkülönültségük szimbolikus-kulturális kontextusokba ágyazódtak, az égi és földi világok vallási világképébe. Teljességük és zártságuk különböző szinteken fejeződtek ki. A két világ rendszerbe való összekapcsolása nemcsak új matematikát hoz, hanem a tudományos megismerés - a természeti törvények új - értelmezését hozza, de még az addigi világkép - benne az ember mint olyan - újragondolását is.
A harmadik példában a korpuszkuláris és hullámelméletek elkülönültségét nemcsak matematikai formalizmusuk határozza meg, hanem alkalmazásaikban sem összevethetők, nem hívhatók elő egyazon megfigyelési helyzetben. Mi több bármiféle erre irányuló kísérlet csak annak bizonyítéka, hogy a beavatkozás a megfigyelés tárgyába nem küszöbölhető ki. Úgy teljesek és zártak, hogy az e rendszerekben megfogalmazott természeti törvények egymás alternatívái.
Mindhárom példa azt mutatja, hogy az elméleti rendszerek belső perspektíváiból nem következik az összekapcsolhatóságuk. Minthogy a természeti törvények kategóriái és összefüggései határozzák meg ezt a perspektívát, de nem értelmezhetők túl ezen, az összekapcsolásra irányuló próbálkozás a belső perspektívához képest szükségszerűen külső. Minthogy ez nem a természeti törvények rendszerében - mint nyelvi rendszerben - jön létre, ezért a nyelvi rendszerből kilépve, fordításként kell ezt a lehetőséget értékelni. A három fordítási helyzet eredménye igencsak különbözik. Az első példában az összekapcsolás összefüggései esetleges hatásokat mutatnak, ezért ezek nem is jelenthetnek természeti törvényeket. Így lehetett azt az értékelést tenni, hogy a mikro- és makrovilág határán a természeti törvények összeomolnak. A második példában az összekapcsolódás olyan összefüggést eredményez, amely független, teljes és zárt rendszert határoz meg vagyis természeti törvényeket ad. A gravitáció törvénye elvontabb mint az összekapcsolódó két rendszer összefüggései, ezért ezek értelmezhetők annak specifikus leképződéseiként. A harmadik példa fordítási helyzete egy fordítási probléma. A meg nem valósítható fordítás alternatív természeti törvényekre enged következtetni. A kvantummechanika ezt az alternatívitást értelmezi olyan összefüggésekben, amelyek függetlenek, teljes és zárt rendszert alkotnának, mégis kérdés az, hogy ez valamilyen természeti törvény megnyilvánulása lenne.
A különböző fordítási helyzetek azt engedik sejtetni, hogy az összekapcsolási műveletek valódi és sajátos történések, és mint ilyenek különböző kimenetelűek lehetnek. Az elméleti-nyelvi rendszereken kívül folytathatók, és kikerülnek az ezeket meghatározó természeti törvények fogalmainak hatálya alól. E történéseket ezért lehet aktusokként értékelni. Ahogyan a nyelvekkel foglalkozó társadalomtudományokban az aktus fogalma azt az alapvető kérdést hordozza: hogyan lehetséges, hogy a nyelven - elméleti rendszeren - kívüli világban egy nyelvi megnyilvánulás valamilyen realitással, megtörténtséggel bír (gondoljunk például egy ígéretre, parancs kiadására, kérésre stb.), úgy a fizikai elméleti-nyelvi rendszerek esetében az alapvető kérdés az, hogy érvényességük határain kívül hogyan kell értelmezni azt, ami ezekkel a rendszerekkel történik.
A fordítási aktusok fogalmától azt várjuk, hogy az összekapcsolások valódi fizikai entitásokra vonatkozzanak: kölcsönhatásokat lehessen értelmezni a különböző világok találkozásán. Ám a példákból láttuk, hogy ezek különböző státuszúak. Az elsőben olyan kölcsönhatással kell számolni, amely nem természeti törvény meghatározottságú (így akár azt a kérdést is föl lehet tenni, hogy a mikro- és makrovilág között "valódi" fizikai kölcsönhatásról van-e szó - ahhoz hasonlatosan, ahogyan meg lehet kérdőjelezni egy ígéret, parancs, kérés stb. érvényességét a nyelvi aktusok, a beszédaktusok körében). A második példában az összekapcsoló összefüggést olyan általánosításként lehetett megadni, amely egy új elméleti rendszert eredményezett (a kölcsönhatások itt természeti törvénynek megfelelőek ahhoz hasonlatosan, ahogyan a jogi ítéletek a jog rendszerében érvényes aktusok). A harmadik példát az a kérdés határozza meg, hogy a kölcsönhatás hiánya lehet-e történés jellegű, ami egyfajta kölcsönhatásként fogható fel (azt gondolom, hogy ez a kvantummechanika paradigmatikus gyökere; jelentősége a nyelvi aktusok azon eseteihez hasonlítható, amikor a meg nem történéseket kell történésekként értékelni: így például a hallgatás valódi kommunikációs esemény lehet, vagy Sherlock Holmes nyomozásában a kutya nem ugatása olyan esemény, amely azt jelentette, hogy a kutya ismerte az éjszaka belopakodó gyilkost).
A fizikai elméletekre vonatkozó kommunikációs értelmezésnek sajátos hozadéka lehet tehát, ha ezek nyelvi rendszerekként való definiálása során e rendszerek közötti viszonyokat tudja értelmezni, a fordítás és aktus fogalmai mentén pedig olyan összefüggéseket keres, amelyeket kölcsönhatásokként lehet azonosítani. Ez a fogalom jól mutatja az elméleti rendszereknek megfelelő világok kapcsolatának kérdéseit.
Az eddigiekben a fordítás és a nyelvi aktus fogalmai alapján mutattam be értelmezési lehetőséget. E fogalmak köznyelvi és intuitív jelentései, úgy tűnt, elegendő perspektívát foglaltak magukban ahhoz, hogy sajátos módon lássuk a fizikai elméletek és részelméletek viszonyait. És bár e fogalmak utalásokat is hordoztak kommunikációtudományi kategorizáltságukra, ezeket nem kellett megnevezni. Ezek után azonban szükséges megnevezni azt az elméleti keretet, ahol ezek a fogalmak szakkifejezések formájában jelennek meg. A két fogalmat többféle elmélet - így kommunikációs, nyelvészeti, kultúratudományi stb. - is definiálja, értelmezi (ezeket most nem fogom ismertetni), jelentéseik sajátosan rögzítettek ezekben a rendszerekben. Lényegében akármelyiket használhatjuk, az értelmezés sajátos lesz az adott elméleti rendszer perspektívájának, kategóriáinak és összefüggéseinek megfelelően. Az alábbiakban a kommunikáció participációs elméletének (PTC) szemszögéből fogom megközelíteni e kérdéseket, azzal a várakozással, hogy ezek fizikai szempontból is értelmezhetők lesznek.
Röviden ismertetem a PTC-t meghatározó, rendszert alkotó alapfogalmakat. Az elméleti keret a ki, mit, hogyan, hol kommunikál kérdések köré összpontosítja az ágens, a kommunikátum, az intézmény és a színtér kategóriáit. A kommunikáció ágensei olyan egységek, amelyek funkciójukban elkülöníthetők a kommunikációs történésekben, és kommunikációs viszony alakul ki közöttük. A kommunikáció során kommunikátumok jönnek létre, vagyis jelentéssel bíró dolgok. A jelentéstulajdonítás a szignifikáció aktusában valósul meg (részletesebben, noha ennek az összefüggésnek az alkalmazását nem fogjuk igénybe venni: a szignifikáció során szignifikánsokhoz szignifikátumok rendelődnek; a szignifikánsok jelentés nélküli dolgok, amelyek, amennyiben utalni tudnak valamire - a szignifikátumra - jelentést kapnak; ez a viszonyulás jön létre a szignifikációban). Az a mód, adott esetben rendszerszerűség, ahogyan az egyes szignifikációk (aktusok) létrejönnek, intézményekként értelmezettek. Intézmények a nyelvi rendszerek, kódok is - intézmények lehetnek az itt nyelvi rendszerekként értelmezett elméletek is. A kommunikáció színterei azok a terek, ahol a kommunikáció végbemegy, vagyis a világnak az a része, ahol jelentések jöhetnek létre.
Ez a kategorizációs keret leginkább a társadalmi kommunikáció jelenségeinek általános leírását tartja szem előtt. Az itteni szempontjainkhoz azonban egy ennél szűkebb értelmezési keretre van szükség, hiszen "csupán" az elméletek és az ezek közötti viszonyok terében szeretnénk maradni, nem tekintjük célnak az elméleteken túli társadalmi világ vizsgálatát. Annyiban azonban igen, amennyiben az elméletekben tükröződnek, megmutatkoznak, reprezentálódnak társadalmi-kulturális elgondolások, mint a bemutatott második példa esetében.
A fenti ki, mit, hogyan, hol kérdéseknek megfelelő fogalmak azonosításához a következő specifikációkat lehet tenni a fizikai elméletekkel kapcsolatos kérdések feltételében: ki a megismerő-megfigyelő (mi a megismerés-megfigyelés egyedi pozíciója), mit hoz létre a megismerés-megfigyelés (mi a jelentéstulajdonítás eredménye), hogyan történik a megismerés-megfigyelés (milyen nyelvi rendszerben történik a jelentéstulajdonítás), hol történik a megismerés-megfigyelés (milyen térfogalom jön létre a jelentéstulajdonítások során, mi a jelentéstulajdonítások tere, világa)?
Az egyes fizikai elméleteket tehát aszerint lehet értékelni, hogy ezek a kérdések hogyan tehetők fel bennük, reprezentációik belső világában. Azonosítani lehet-e az ágens, a kommunikátum, a nyelvi rendszer (az intézményt specifikálva) és a színtér fogalmait? E fogalmak megfelelő kategorizációt és összefüggéseket adnak-e a fordítás és a nyelvi aktus fogalmainak perspektívájában felmutatott értelmezésekhez? Végső soron: a fizikai elméletekkel kapcsolatos kérdések kommunikációs elméletbe fordítása adhat-e valamilyen sajátos többletet? Egy egyszerűnek tűnő példán szemléltetetem az alkalmazás lehetőségét.
Az alábbi példa Einstein speciális relativitás elméletéhez kapcsolódik (1. ábra). Képzeljünk el két űrhajót (A, B), amelyekben egy-egy megfigyelő tartózkodik. A űrhajó nagyon közel, egyenes vonalú és egyenletes mozgással halad el B mellett. A két űrhajó közötti kis térben az űrhajók egyik végénél eltűnik egy töltés (x esemény), és ugyanabban a pillanatban megjelenik a másik végénél (y esemény), tehát érvényesül a töltésmegmaradás törvénye, vagyis a töltések összege nem változik. Tételezzük fel, hogy az eltűnést és előtűnést fényvillanás kíséri, így észlehetők a megfigyelők számára. Tudva azt, hogy a fény véges sebességgel érkezik a megfigyelőkhöz, B megfigyelőnek az űrhajó közepére kell állnia, ha azt szeretné, hogy az egyidejű eseményekről egyidejűleg jussanak el hozzá a fényjelek. Tegyük fel, hogy a jelenség bekövetkezte pillanatában A űrhajó pontosan B mellett áll, és az egyidejű események megfigyeléséhez az A űrhajóbeli megfigyelő is középen tartózkodik. Ám amíg hozzá elérnek a fényjelek, űrhajója kissé továbbhalad. Az x eseményről hamarabb érkezik a jel, mint y eseményről. Így azt érzékelheti, hogy a töltés eltűnt az egyik helyen és még nem jelent meg a másik helyen. Arra a következtetésre juthat, hogy a mozgó űrhajóban, bár csak egy rövid időre, nem teljesül a töltésmegmaradás törvénye, a töltések összege megváltozott. Nem biztos, hogy a természeti törvény érvénytelenségére vonatkozó megállapítása végérvényesen cáfolható.
1. ábra
|
Az űrhajók helyzete az események bekövetkezésekor
|
. |
Az űrhajók helyzete, amikor B észleli az
eseményeket [2]
|
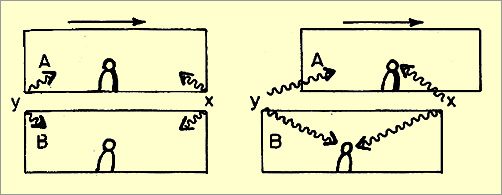
A megfigyelő értékelheti úgy is a helyzetet, hogy "valójában" érvényes a töltésmegmaradás törvénye, csak tekintetbe kell venni a megfigyelés körülményeit, nevezetesen azt, hogy az űrhajója mozog, a megfigyelhetőséget biztosító fényjelek pedig különböző idők alatt érnek el a megfigyelőhöz. Lényegében külön kell választani tehát a jelenséget és a megfigyelt jelenséget. Ez utóbbi esetben a megfigyelés körülményeit - a mozgást - is tekintetbe kell venni, és eszerint korrigálni a megfigyelési adatokat. Így a természeti törvények érvényessége általános marad. Lényegében ez a klasszikus fizika logikája, amely a véges sebességű fény közvetítésével történő megfigyelés problémájával találkozott.
Amilyen egyszerűnek tűnik azonban a megoldás, éppen olyan megoldhatatlan filozófiai kérdést is felvethet: ha a mozgó űrhajók adatait korrigálni kell, a megfigyelés hitelesen csak nem mozgó körülmények között tehető meg. Léteznie kell egy olyan abszolút vonatkoztatási rendszernek, amelyhez viszonyítani lehet a mozgó űrhajók adatait és a szükséges korrekciókat. Honnan tudható, hogy valami abszolút mozdulatlan? A űrhajós ugyan látja, hogy elhalad B mellett, de B is ugyanezt látja A-val kapcsolatban. Ugyanez a kölcsönös relativitás fennáll minden objektumra a világban. Kézenfekvő válasz a fentiek alapján az lenne, ha állónak tekinthető az az űrhajó, amelynél - korrekció nélkül - teljesülnek a törvények, és mozgónak az, amelynél nem.
Akkor most végezzük el a fenti kísérleteket úgy, hogy az egyidejű események ne az űrhajók közötti résben menjenek végbe, hanem a két űrhajó belsejében. Azt várnánk, hogy ha B űrhajó áll, akkor egyidejűen jelennek meg a felvillanások a megfigyelő számára, ha pedig mozog, akkor nem. Valójában nem ez történik. Az űrhajók belsejében mindkét esetben egyidejűnek látszanak. Mindkettőben teljesül a töltésmegmaradás törvénye a megfigyelők észlelésében. (A paradoxon mögött az áll, hogy a mozgó űrhajóban a fény sebessége nem lesz más, pl. az y-ból érkező fény nem tűnik lassabbnak az űrhajó mozgása miatt.) Általánosságban: semmilyen kísérlettel nem dönthető el az űrhajóban, hogy az mozog vagy sem, mozgásállapotától függetlenül teljesülnek a természeti törvények. Végső soron: a természeti törvények lokálisan igazak. A különböző lokalitások között összefüggés adható meg (itt a relatív sebességgel). Lényegében ez a speciális relativitáselmélet alapja. A példa vázlatosan szemlélteti a klasszikus fizika zsákutcáját, és egy új elmélet, a relativitáselmélet létrejöttét.
Értelmezzük kommunikációs szempontból azt, amit a fenti példa szemléltetett. A fizika megközelítésmódjához képest ez bizonyosan alternatív értelmezés lesz a 4. részben megfogalmazott diszciplináris sajátosságok miatt. A különbség abban gyökerezik, hogy míg a fizika a természeti törvények megfogalmazását célozza, addig egy kommunikációs kutatás a természeti törvények jelentésével foglalkozna. Míg előbbinek paradigmatikus meghatározója az, hogy egy a megfigyelőtől független rendszert adjon, elvonatkoztasson a megfigyelőtől, addig utóbbi paradigmatikusan nem tekinthet el a jelentések létrehozójától, a megfigyelőtől és annak helyzetétől. Ennek a kommunikációs alapállásnak a következőképpen kell relevánsan a kérdést feltennie: a megfigyelés partikuláris ágense hogyan hoz létre olyan jelentéseket, amelyekben el tud vonatkoztatni saját partikularitásától?
Tekintsük először a példa "előzményét", amikor a megfigyelő szemmel végzi a megfigyeléseket, így nem kell számolni a fény sebességével (amit csak a szemnél sokkal érzékenyebb műszerek mutatnak), a jelenségek B űrhajóban játszódnak, amit az űrhajós mozdulatlannak érzékel. A megfigyelőt azonosíthatjuk a megfigyelés ágenseként, az űrhajó belsejét pedig a megfigyelés és értelmezés színterének. Minthogy a megfigyelő nem érzékeli a fényjelek véges sebességét, így bárhol áll, egyidejűnek érzékeli a két felvillanást. A töltésmegmaradás törvényét egyedi helyzetétől függetlenül érzékelheti. Így lényegében a megfigyelés aktusában elvonatkoztathat a partikuláris pozíciójától. A megfigyelések színtere nemcsak az űrhajó belsejét jelentheti, hanem kiterjeszthető addig, ameddig a megfigyelések ilyen módon hitelesek.
Kommunikációs szempontból az ágens azonban nem csupán a fizikai világ egy pontja, amelynek a felvillanások tükrözésének fizikai tulajdonságával kell bírnia. Az ágens ugyanis nem csupán ezeket, hanem az ezeket meghatározó természeti törvényeket "tükrözi", úgy hogy a két felvillanásnak tulajdonít elvontabb jelentést. Ehhez pedig arra van szükség, hogy valamilyen elmélete legyen az ilyen típusú eseményekről. Azaz valamilyen nyelvi - szignifikációs - rendszernek a birtokában van. Ez teszi különlegessé ebben a fizikai világban, valójában egyedivé. (Most tekintsünk el attól hogyan jött létre ez a szignifikációs rendszer, és az egyszerűség kedvéjért tételezzük fel azt, hogy ilyen típusú felvillanásokat csak töltés-jelenségek okozhatnak.)
Az ágens lényegében akkor fogja fel mit is látott, ha a megfigyelt jelenséget valamilyen természeti törvény megnyilvánulásaként látja. A természeti törvény jelentését akkor adhatja meg, ha ezt függetlenként, hatókörét pedig teljesként és zártként rögzíti. Vagyis megrajzolja azt a világot, amelyet a természeti törvények határoznak meg, miközben jelentés nélküli a természeti törvények általánosságán túli "nem-világ". Az ágens a két felvillanást egy jelentéssel bíró világ részeként "tükrözi". Az ágens perspektívájából a világnak ezt a terét nevezzük színtérnek. Ezen a színtéren nyer értelmet az ágens ágens-mivolta is. Ezt a megfigyelés képessége jelenti, és nem tud létezni számára a megfigyelhető világon túli, valamilyen eleve megfigyelhetetlen világ. A színtér fogalma ilyen értelemben nem egy nyersen fizikai tér, hanem szimbolikus, jelentésteli, nevezhetjük szignifikációs térnek. Ebben a térben lehetséges elvonatkoztatni az ágens megfigyelői helyzetétől.
Mint az előző példában, legyen most lehetősége a megfigyelőnek a fény sebességét érzékelnie, például valamilyen berendezés segítségével. Erőteljes változás áll be az ágens perspektívájában a fényjelek által megtett útvonalak különbségéből adódó különböző beérkezési időpontok miatt: az egyidejű események megfigyelésének érvényessége leszűkül a középvonalra. Így az ágens vagy lemond a világ többi részéről, és a jelentésteliség színterét itt rajzolja meg, vagy a jelentésteliség jelentését, a szignifikációs rendszert kell újra értelmeznie. Nyilvánvaló, hogy csak a második megoldás elfogadható (az első eset valójában egy nyílt rendszert jelent). Az ágens számára a középvonal lehet a vonatkoztatási alap, ahol "magától értetődően" jelentésteliek a természeti törvények. A fény sebességének figyelembe vételével azonban az ettől eltérő pozíciókhoz korrekciós együtthatókat lehet rendelni. Ezt a korrekciós együtthatót akár a megfigyelő berendezésbe is be lehet építeni. A megfigyelések terét, amelyet az űrhajó belseje jelenti, ki lehet terjeszteni a világra, ahol a megfigyelések hitelessége ilyen módon biztosítható. Így helyreáll a természeti törvényekre vonatkozó kritériumoknak való megfelelés, a szignifikáció színtere újra zárt és teljes lehet. Ebben a megfigyelő partikuláris helyzetétől a természeti törvények függetlensége értelmében újra el lehet vonatkoztatni. Bár a megoldás korrekciósnak, technikainak tűnik, valójában fordításként is lehet értékelni: fordításként, amely megadja, hogy hogyan kell leképezni általánosan az ágens partikuláris helyzetének megfelelő szignifikációkat egy szűkebb szignifikációs helyzetre, amelyet vonatkoztatási alapnak jelölt ki az ágens (a középvonalra).
Hasonló eljárással lehet kezelni a példa eltérő sebességes helyzetét is. Az ágens itt is kijelöl egy vonatkoztatási alapot, amelyhez képest azokat a jelenségeket le lehet képezni, amelyekhez különböző sebességértékek adódnak. A korrekciós együttható beépítésével a megfigyelések színterét ki lehet terjeszteni az űrhajó határain túl a teljes térre, az ágens partikuláris helyzetétől pedig el lehet vonatkoztatni.
Láttuk azonban, hogy a megfigyelések a másik űrhajóban is hitelesek, a természeti törvények igaznak bizonyulnak, és akár a másik űrhajós is egyfajta korrekciós eljárással kiterjesztheti a jelentésteliségek színterét a teljes térre. Ez ellentmondás. Matematikailag ez határozatlanságokat eredményez, szempontunkból pedig azt lehet megállapítani, hogy ebben a helyzetben az ágenstől való elvonatkoztatás nem lehetséges. A megfigyelhető természeti törvények lokálisan igazak, összevetésük valamilyen általánosított, kiterjesztésen alapuló rendszerben pedig problémát jelent. Más megfogalmazásban: a lehetséges ágensek szignifikációs rendszerei közötti fordítás már "nem magától értetődő", technikai megoldással nem biztosítható.
Eddig a klasszikus fizika szempontja jelent meg az értelmezésünkben. Logikája az volt, hogy a természeti törvények a definíciónak megfelelően teljes általánosíthatósággal adhatók meg, és ez biztosította a megfigyeléstől való függetlenségét is. Lényegében azt kellett feltételezni, hogy a természeti törvények nem lehetnek lokálisan, így a megfigyelés partikularitásában igazak. Ehhez képest a relativitáselmélet egy egészen más megközelítési módot ad, és ez a kommunikációs - ágens perspektívájú - értelmezésnek is érdekes vonatkozást nyújt, amikor a természeti törvények lokalitásából kell kiindulni. A megfigyelés így e lokalitásokhoz kapcsolódik, ilyen értelemben partikuláris, és az ágens lokalitásban rögzített pozíciójától nem lehet elvonatkoztatni. Az egyes űrhajósok megfigyelései mind igazak, még akkor is, ha a másik űrhajóról nézve a jelenségek másként néznek ki (a saját űrhajóban detektált egyidejű események a másik űrhajóból nézve nem azok). Mintha e lokalitásokból kilépve a természeti törvények torzulnának. Einstein elképzelése az volt, hogy amennyiben e torzulások szimmetrikusak, vagyis az egyik űrhajóból a másikra nézve tapasztalt eltérések ugyanolyan értékűek, mint fordított esetben, úgy ezt általános összefüggésként természeti törvényként lehet rögzíteni (a speciális relativitáselméletben ez a Lorentz-transzformáció), amely a lokalitások "felett áll" - pontosabban köztük. Vagyis: a természeti törvények egyik lokális világából egy másik lokális világába történő átmenet során törvényszerű "torzulások" történnek. Szempontunkból e "torzulások" voltaképpen olyan fordítási műveletekben fejezhetők ki, amelyek a lokálisan rögzített szignifikációs rendszerek közötti "átmenetet" adják meg.
A lokalitások közötti szimmetriát a bemutatott példa úgy jeleníti meg, hogy az egyes űrhajósok a maguk űrhajójában felismerték a természeti törvények érvényességét, utána tapasztalták a másik űrhajóban a felvillanások közötti eltéréseket, majd miután felvették egymással a kapcsolatot, egyeztették, hogy ezek az eltérések ugyanolyan mértékűek. Ez tulajdonképpen a fizikai megközelítésmód modellezése. Eszerint a leírandó világ egészében kijelölhetők azok a lokalitások, amelyek lefedik a teljes teret (ez a világegyetemet lefedő űrhajók tereivel modellezhető), illetőleg ezen lokalitások között meghatározhatók a törvényszerű összefüggések, amelyek kölcsönhatások formájában nyilvánulnak meg (ezt az egyes űrhajók utasainak a másik terére vonatkozó eltérések az egyeztetése jelképezi). Ebben mutatkozik meg a természeti törvények függetlensége, terének teljessége és lefedettségének zártsága.
Mindezt úgy lehet látni, hogy a természeti törvényekre irányuló megfigyelés és a megfigyelés partikularitásától való elvonatkoztatás úgy biztosítható, ha az egyedi ágens önmagát és űrhajóját megsokszorozhatja az előbbi módon. Kommunikációs szempontból azonban a megismerést az ágens egyedi és partikuláris pozíciójából, nyelvi perspektívájából kell modelleznünk. A klasszikus fizikára vonatkozó példáknál ehhez kézenfekvő volt az ágens abbéli felismerése, hogy kijelölhető egy "egyedi" abszolút vonatkoztatási rendszer, amelyhez képest a megfigyelések és értelmezések kivitelezhetők voltak. A relativitáselméletben és a modern fizikában azonban egy ilyen "kiindulópont" nem feltételezhető - a lokalitások mind "kiindulópontot" kínálnak. A kérdés tehát az, hogy az egyedi ágens lokalitása hogyan tudja leképezni a többi lokalitást.
A természeti törvényekre irányuló megfigyelések az ágens egyedi pozíciójából történnek. Az ágens megfigyeléseinek érvényessége annak a szignifikációs rendszer perspektívának függvénye, amelynek segítségével az egyedi megfigyeléseket általános összefüggésekben értelmezi. Ezek az általános összefüggések természeti törvényeket határoznak meg, amelyek úgy tudnak általánosan vonatkozni, hogy ezek az összefüggések függetlenek, rendszerük teljes és zárt. Ez az összefüggésrendszer rajzolja ki a jelentésteli világot, a szignifikatív megfigyelhetőség terét, színterét.
A természeti törvények a modern fizikában lokálisan igazak. Ez azt jelenti, hogy bár az ágens szignifikációs rendszere teljes és zárt (egy matematikai rendszer nem is lehet más), amely egy határtalan világot mutat (hiszen nem értelmezhető e határon túli világ), ez az adott szignifikációs rendszer belső perspektívája, amely egy egyedi ágens sajátja. Külső perspektívája értelmezhetetlen a szignifikációs rendszer belső perspektívájából (olyan mintha természeti törvényekként kellene természeti törvényekként értelmezhetetlen jelenségeket értelmezni). Amennyiben az ágens szignifikációs rendszerének vonatkozását lokálisként feltételezi, olyan lokalitásokat, színtereket kell feltételeznie perspektíváján kívül, amelyekre szintén szignifikációs rendszerek vonatkoznak, de ezek fordítás útján érhetők el. Feltételezhető, hogy a lokalitások között kölcsönhatások vannak, mégpedig olyanok, amelyek az ágens szignifikációs rendszerében nem értelmezhetők (amennyiben értelmezhetők lennének, a természeti törvények összefüggéseinek kiterjesztését lehetne eszközölni). E "furcsa" kölcsönhatások az ágens szignifikációs rendszerének külső perspektívájában megfogalmazható fordítási aktusok és összefüggések mentén értelmezhetők. A cél természetesen az, hogy ezeknek olyan rendszerét lehessen megadni, amely teljes és zárt, az alapösszefüggéseik függetlenek - ebben az esetben a fordítási műveletek szignifikációs rendszerbe illeszkedők, a kölcsönhatások természeti törvényeknek megfelelően értelmezhetők (ebben sikeres volt a speciális relativitás elmélet, a korábbi példákban a gravitációs elmélet, de problémás volt a buborékkamra esetében megnyilvánuló elméletek viszonya és paradoxonként jelent meg a korpuszkuláris és hullám elméletek összekapcsolási kísérlete).
Mindazonáltal ez a kommunikációs megközelítés ellentétes a fizikai elméletek önértelmezésével. A fizikai elméletek olyan kategória és összefüggésrendszerek, amelyek természeti törvény megfogalmazásai nem lehetnek függvényei a megfigyelés ágense egyediségének és partikularitásának. Ez utóbbinak levezethetőnek kell lennie az előbbiből, a megfigyelési lehetőségeket ezeknek az általános összefüggéseknek a specifikációi adják meg. A kommunikációs perspektíva fordított, hiszen a megfigyelő és megismerő ágens fogalmából indul ki, és annak lehetőségeit vizsgálja, hogy egy hozzárendelt szignifikációs rendszer használatával miként jelölheti ki a természeti törvények színterét, és ebben hogyan sikerül az elvonatkoztatás saját egyedi és partikuláris helyzetétől, azaz hogyan juthat el egy elmélet megformálásáig.
A kommunikációs megközelítés lehet módszertani jelentőségű, amely egy elmélet megformálódása előtti mozzanatait, állapotait tárja fel. Ez a perspektíva abban lehet érdemleges, hogy képes lehet értelmezni a természeti törvények lokálisan értelmezett általánosságán túli kölcsönhatásokat. Olyan alapproblémákra is tekintettel lehet, mint amilyet a kvantummechanika jelenít meg: a szükségszerűen beavatkozó megfigyelés mint kölcsönhatás problémájára. Itt ugyanis valódi kérdés, hogy a korpuszkuláris és a hullám elmélet dualitása a beavatkozó megfigyelő-értelmező ágensnek vagy a természeti törvényeknek tulajdonítható.
[1] A kísérletet egy kissé leegyszerűsítve vázoltam, hogy az eredmény lényegét kiemeljem. Valójában az elektronok hullámtermészete akkor mutatkozik meg, ha két ablakot használunk. Ekkor az egyes elektronok egyik vagy másik résen áthaladva "bekanyarodnak" a kijelölt keret mögé és olyan eloszlást mutatnak, amely interferenciajelenségeket produkáló hullám formájú.
[2] Az ábra forrása: Feynmann, 1983, 103, 151.
Bajnok A. - Korpics M. - Milován A. - Pólya T. - Szabó L. (2012) A kommunikatív állapot. Diszciplináris rekonstrukciók. Budapest: Typotex.
Bohr, N. (1984) Atomfizika és emberi megismerés. Válogatott tanulmányok. Budapest: Gondolat.
Csaba F., szerk. (2003) A matematika filozófiája a 21. század küszöbén. Válogatott tanulmányok. Budapest: Osiris.
Einstein, A. (2003) A speciális és általános relativitás elmélete. Budapest: Kossuth.
Feynmann, R. (1983) A fizikai törvények jellege. Budapest: Magvető.
Forrai G. - Szegedi P., szerk. (1999) Tudományfilozófia. Szöveggyűjtemény. Budapest: Áron.
Hamp G. (2006) Kölcsönös tudás. Kommunikáció és megismerés. Budapest: Typotex.
Heisenberg, W. (1967) Válogatott tanulmányok. Budapest: Gondolat.
Hernádi M., szerk. (1984) A fenomenológia a társadalomtudományban. Budapest: Gondolat.
Horányi Ö., szerk. (2007) A kommunikáció mint participáció. Budapest: AKTI-Typotex.
Horányi Ö. (2009) Arról, ami szignifikatív és arról, ami kommunikatív; valamint arról, ami problematikus (szinopszis, 7.3 változat). In Bagdy E. - Demetrovics Zs. - Pilling J. szerk., Polihistória. Köszöntők és tanulmányok Buda Béla 70. születésnapja alkalmából. Budapest: Akadémiai, 201-235. Elérhető interneten: http://ozseb.horanyi.hu/participacio/szinopszis7_3.htm
Laki, J., szerk. (1998) Tudományfilozófia. Budapest: Osiris-Láthatatlan Kollégium.
Neumann J. (1965) Válogatott előadások és tanulmányok. Budapest: Közigazgatási és Jogi.
Pléh C. - Siklaki I. - Terestyéni T., szerk. (1997) Nyelv, kommunikáció, cselekvés. Budapest: Tankönyvkiadó.
Quine, W. V. (2002) A tapasztalattól a tudományig. Válogatott tanulmányok. (szerkesztette és válogatta Forrai G.), Budapest: Osiris.
Searle, J. R. (1998) Mind, Language and Society. Philosophy in the Real World. Basic. Magyarul: Elme, nyelv és társadalom. A való világ filozófiája. Budapest, Vince, 2000.
Simonyi K. (2011) A fizika kultúrtörténete. Ötödik, javított, bővített kiadás, Budapest: Akadémiai Kiadó.
Wigner J. (2005) Wigner Jenő válogatott írásai. (válogatta Ropolyi L.) Budapest: Typotex.