Barabási Albert-László: Behálózva. A hálózatok új tudománya.

A kommunikáció elmélet megnevezése:
A hálózati kapcsolatok elmélete.

Az elmélet érvényességi területe:
Ezen elméletnek számos érvényességi területe van. Barabási könyvében csak néhányra találunk példát, de az elméleten elgondolkozva számos új területen alkalmazhatjuk az ott leírtakat.

Az elméletben érvényesülő kommunikáció-fogalom típusa:
Az elmélet nem alkalmaz előzetesen ismert kommunikáció-fogalmat.

Az elmélet leíró vagy magyarázó:
Az elmélet magyarázó jellegű.

A koncipiálásba bevont szerkezeti egységek:
A hálózat felépítésének kutatását a hálózat alapvető komplexitásának vizsgálata előzi meg. Barabási szerint a világban bármerre nézünk, találhatunk hálózati működésre utaló jeleket, mely hálózatok legtöbbje komplex hálózat.
Korábban Erdős Pál és Rényi Alfréd matematikusok nyomán a gráfelmélet elsősorban a véletlen kapcsolatok vizsgálatával foglalkozott, ahol az egyes pontokhoz tartozó kapcsolatok száma Poisson-eloszlású. Barabási arra mutat rá, hogy a nem-szabályozott módon, azaz természetesen fejlődő rendszerekben a kapcsolatok nem véletlenül alakulnak ki, az újonnan érkezők jellemzően a korábbi kapcsolati központokhoz kapcsolódnak. A természetben és a társadalomban fellelhető legtöbb kapcsolatháló ezért nem Poisson, hanem hatványfüggvény eloszlású lesz. A Poisson- és a hatványfüggvény-eloszlású kapcsolathálók közti különbség érzékeltetésére Barabási számtalan szemléletes példát hoz több diszciplína területéről is. Ezen példák között gazdasági, közlekedési, biológiai és informatikai példák is találhatóak.
Ezen példák után már meghatározható a hálózatok skálafüggetlenségének definíciója:
"A hatványfüggvények azt a tényt fogalmazzák meg matematikailag, hogy a valódi hálózatokban a pontok többségének csak néhány kapcsolata van és ez a számtalan kis pont együtt létezik néhány nagy középponttal, olyan pontokkal, amelyekhez szokatlanul sok kapcsolat tartozik.

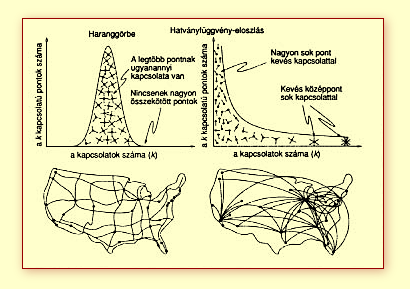
A véletlen és a skálafüggetlen eloszlású hálózatok

A véletlen hálózatokban a fokszámeloszlás csúcsa azt mutatja, hogy a pontok nagy részének ugyanannyi kapcsolata van, és az átlagtól eltérő pontok rendkívül ritkák.
Ezért a véletlen hálózatban a pontok fokszámának van egy jellemző nagysága, egy skálája, amelyet a fokszámeloszlási grafikon csúcsa határoz meg, és amelyet egy átlagos pont segítségével képzelhetünk el. Ezzel szemben a hatványfüggvény esetében az eloszlás csúcsának hiánya arra utal, hogy a valódi hálózatokban nincsen tipikus pont. A pontok folytonos hierarchiáját figyelhetjük meg, amely a kevés középponttól a sok pici pontig terjed. A legnagyobb középpontot két vagy három, valamivel kisebb középpont követi szorosan, majd egy tucat még kisebb következik, és így tovább, végül elérkezünk a sok kis pontig.
A hatványfüggvény szerinti eloszlás tehát arra kényszerít bennünket, hogy teljesen lemondjunk a skála vagy a jellemző pont fogalmáról. (…) Ezekben a hálózatokban nincsen belső skála. Ezért kezdte csoportom skálafüggetlen hálózatként említeni a hatványfüggvény-eloszlású hálózatokat" (Barabási 2003).
Vagyis minden hálózatban lesznek egyedek (ágensek) melyek kivételesen sok és erős kapcsolattal rendelkeznek (ezek száma természetesen a hálózat egészéhez viszonyítva kicsi), és olyanok, melyek csak néhány, esetleg egy kapcsolattal bírnak.

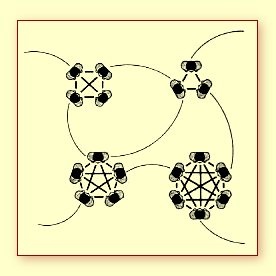
Azt, hogy a sok kapcsolattal rendelkező központok, mint amilyeneket az Interneten is találhatunk (pl.: a Yahoo), miért váltak központtá, Barabási többféleképpen magyarázza. Egyrészt magyarázat lehet a hálózatban való részvétel idejének hossza. Vagyis aki előbb jött, az szerezheti meg a kapcsolatok többségét, így válva központtá. Azonban az Internet esetében a Google az egyik olyan internetes központ, mely sokkal később tűnt fel az Internet hálójában, mára mégis az egyik legnagyobb központ lett. Másrészt további magyarázat lehet a "népszerűség alapján történő kapcsolás elve". Ez annyit tesz, hogy ha egy ágens bármely hálózatban csatlakozni akar a másikhoz, annak alapján teszi, hogy megvizsgálja, rajta kívül már hányan kapcsolódtak, illetve ennek alapján hova érdemes kapcsolódni. Barabási minden központnak meghatároz egy alkalmassági számot. Ez a szám minél magasabb, annál nagyobb a valószínűsége, hogy az adott központ további számos kapcsolathoz juthat hozzá. Annak valószínűsége, hogy egy k kapcsolatú és h alkalmasságú ponthoz kapcsolódjunk:

Mint látszik, Barabási és kutatócsoportja a skálafüggetlen rendszerek tulajdonságainak leírásával is részletesen foglalkoztak. Egyik fontos megállapításuk a rendszer robosztusságára vonatkozik. "Egy (véletlen) hálózat csomópontjainak a meghibásodása a hálózatot könnyen széttördelheti elszigetelt, egymással nem kommunikáló részekre. (…) Skálafüggetlen hálózatból (viszont) véletlenszerűen eltávolítható a pontok jelentős része anélkül, hogy a hálózat széttöredezne. A skálafüggetlen hálózatok korábban nem sejtett hibatűrő képessége egy, a véletlen hálózatokétól eltérő tulajdonság. Mivel az Internetről, a világhálóról, a sejtről és az ismeretségi hálózatokról tudott, hogy skálafüggetlenek, ezek az eredmények azt jelzik, hogy a hibákkal kapcsolatban jól ismert ellenálló képességük, topológiájuk belső tulajdonsága". E gondolat szerint tehát a néhány nagy forgalmú központ is egyben tartja a rendszert, ha a rendszer elemeinek nagy része véletlenszerűen megsemmisül. Szándékos támadásokkal szemben azonban ezek a rendszerek védtelenek. Az Internet esetében (de organikus szervezetek, hálózatok esetében is) ilyenek a rendszert speciálisan támadó vírusok, valamint az egyes szerverek, központok elleni hacker támadás típusok (DoS, Teardrop, PoD, stb.).
Ez a sebezhetőség betudható annak is, hogy az Internet amit ma használunk egyáltalán nem hasonlít arra az elosztott, egyenrangú hálózatra, amit Paul Baran a Rand Corporationnál elképzelt a '60-as évek végén.

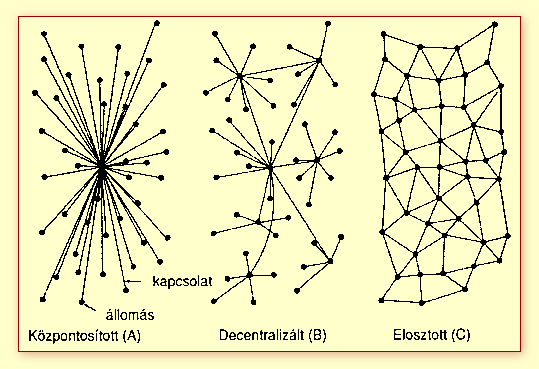
Vagyis, hogy a hálózat természetes módon az egyenrangú eloszlás felől a skálafüggetlen eloszlás felé fejlődött.

A koncipiálásba bevont színterek, a koncipiálásba bevont dinamikák:
Barabási elméletének egyik talán legérdekesebb része - azon túlmenően természetesen, hogy tiszta logikával és számtalan példával bizonyította a skálafüggetlen hálózatok létét és gyakoriságát -, hogy a kapott kutatási eredmények alapján megpróbálta felrajzolni az Internet kapcsolati hálójának általános térképét. Maga a kísérlet nem új, hiszen valami hasonlóval már találkozhattunk Castellsnél is, de ebből a perspektívából újabb válaszokat kaphatunk kérdéseinkre.

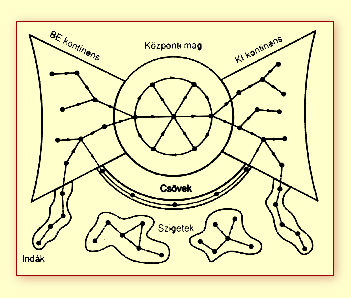
Ezen térkép szerint, az Internet központi magját, amelyet számos kapcsolat jellemez, különböző tulajdonságú mezők veszik körül. Vannak melyek csak hivatkoznak a központra, de onnan link nem mutat vissza. Vannak olyan területek a neten, ahol a helyzet pont fordított, a központnak van kapcsolata kifelé, de visszafele nem lelhető fel kapcsolat. Az ún. indákon "lógó" számítógépek egymáson keresztül, közvetetten kapcsolódnak a központi maghoz. Végül találhatunk az Interneten elkülönülő szigeteket, melyekből nem mutat kapcsolat a szigeten kívülre, függetlenül attól, milyen a sziget belső kapcsolatsűrűsége. (Ennek függvényében érthető miért mutat a weblapom látogatottsága egyre mókásabb adatokat.)
Ami talán az elméletből hiányzik, ám jó alapja lehet egy következő gondolatmenetnek a kapcsolatok minőségének vizsgálata. Vagyis, hogy nem mindig szerencsés a kapcsolatok minőségét egyenrangúnak tekinteni, hiszen ez nem biztos, hogy mindig helytálló eredményekhez vezet.

Az elmélet kapcsolata más elméleti konstrukciókkal:
Az elméletet a szociológia tudományán belüli kutatásokkal lehet összekapcsolni. Barabási négy szociológiai kutatásról ír: a "kis világ" kapcsán Stanly Milgram, a gyenge kapcsolatok ereje kapcsán Mark Granovetter, végül a hibrid kukorica illetve a tetracyclin kapcsán Bryce Ryan, Neal C. Cross, Elihu Katz, James Coleman és Herbert Menzel munkássága kerül bemutatásra. Néhány szociológia folyóirat szerint azonban Barabási elméletének teljességéhez azonban szükséges lett volna további elméletek körüljárása is. Úgymint a network dinamikával foglalkozó Franz Stokman, a hálózati központiság mérőszámait kidolgozó Phillip Bonacich, strukturális lyukakkal is foglalkozó Ronald Burt, a kapcsolathálók vizualizációján dolgozó Linton C. Freeman.

Az elméletalkotás célja:
A cél annak megértése, hogyan kapcsolódhatnak össze az Interneten a számítógépek, az először kaotikus összevisszaságnak látszó (vagy véletlenszerűnek ható) hálózat valójában milyen rendezőelvek mentén épül fel. További cél azon tézis bizonyítása miszerint az ilyen bonyolult hálózatok legtöbbször skálafüggetlenek, vagyis nem véletlenszerűek, és végképp nem egyenrangúak, ahogy azt például az első fejlesztők szerették volna. Ebből kiindulva aztán eljuthatunk olyan tudományterületek részletesebb vizsgálatáig, ahol szintén fontos szerep jut a hálózati kapcsolatoknak.

Az elmélet eredeti alkalmazási terepe:
Az eredeti alkalmazási terep elsősorban az Internet, a vizsgálatok nagyobb része is itt zajlott, de sikeresen alkalmazható sok egyéb tudományterületen is. A szociológia és a pszichológia területén már több mint egy évtizede foglalkoznak a kapcsolatháló elemzéssel, melyben ez az elmélet új fejezetet nyithat.

Az elmélet háttérdiszciplínái:
Informatika, szociológia, sejtbiológia

Néhány fontosabb bibliográfiai tétel:
Barabási Albert-László: Behálózva. A hálózatok új tudománya. Magyar Könyvklub. Budapest. 2003

Az összefoglalót készítette: Barkóczy László
Dátum: 2003. december 10.