Claude E. Shannon - Warren Weaver

A kommunikáció elmélet megnevezése:
A kommunikáció matematikai elmélete.

Az elmélet érvényességi területe:
Technikai (elsősorban elektronikus) rendszerek adatátvitele, kommunikációja.

Az elméletben érvényesülő kommunikáció-fogalom típusa:
A kommunikációt, mint folyamatot, a matematikai tudomány felől közelíti meg, az elméletben vizsgált kommunikációs folyamatokat matematikai levezetésekkel bizonyítja, illetve támasztja alá.

Az elmélet leíró vagy magyarázó:
Az elmélet leíró jellegű.

A koncipiálásba bevont funkciók:
Weaver a hírközlési problémák három szintjét különbözteti meg:

A szint - Technikai probléma. Milyen pontosan vihetők át a hírközlési szimbólumok?
B szint - Szemantikai probléma. Az átvitt jelek mennyire pontosan tükrözik a kívánt jelentést?
C szint - Hatékonysági probléma. A vett jelentés milyen hatékonysággal váltja ki a kívánt hatást?

Shannon és Weaver elméletében nem szerepel a B és C szint kifejtése, de úgy vélik az A szint alapos elemzésével és a felmerülő problémák (sávszélesség, zaj, a kódolás milyensége) megoldásával, a másik két szint is megoldhatóvá válik. A legfőbb probléma, hogy egy adott ponton hibátlanul vagy megközelítőleg hibátlanul reprodukáljunk egy másik pontról küldött jel- vagy szimbólumsorozatot. Másrészt, a tényleges csak egy a lehetséges jel- vagy szimbólumsorozatok közül. A rendszert úgy kell megtervezni, hogy ne kizárólag a kiválasztott, hanem a potenciális üzeneteket is kezelje.

A koncipiálásba bevont szerkezeti egységek:
Shannon hírközlési sémájának vázlata a következőképpen rajzolható fel:

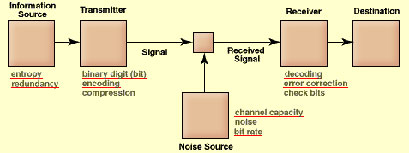
Az információforrás (Information source) egy sor lehetséges közül választja ki a kívánt üzenetet. Maga a kiválasztott üzenet hangot, zenét, írott szöveget, képeket stb. tartalmazhat. Az adó (transmitter) ezt az üzenetet jellé (signal) alakítja, amely egy hírközlési csatornán keresztül jut el a vevőhöz (receiver). A vevő egy fajta fordított adó, mely a vett jeleket visszaalakítja üzenetté, és továbbítja a rendeltetési helyére (destination). Az átviteli folyamat jellegzetessége, hogy a jelhez olyan dolgok is hozzá adódnak, melyeket az információforrásnak nem volt szándékában előállítani. Ilyenek lehetnek a hangtorzulások, zörejek, hibák az átvitelben stb. Az átvitt jelben létrejövő minden változást zajnak (noise source) nevezünk.

A koncipiálásba bevont színterek, a koncipiálásba bevont dinamikák:
Shannon elméletében az információ kifejezést speciális értelemben használjuk. Nem arra vonatkozik, amit mondunk, hanem amit mondhatunk, "azaz az információ egy üzenet kiválasztásában rejlő szabad választásunk mértékét jelöli". Az információ mennyiségét pedig a rendelkezésre álló választási lehetőségek számának kettes alapú logaritmusával mérjük. Így számolva megkapjuk a az információ alapegységét, melyet "bit"-nek nevezünk (binary digit).
Az üzenet előállításában nagy szerepet játszik a valószínűség. Ez bármely nyelvben is megtalálható. Ezek az előfordulási valószínűségek bizonyos fokig szabályozzák is a nyelvet. Az olyan rendszereket, melyek valamilyen valószínűség szerint szimbólumok sorozatát állítja elő, sztochasztikus folyamatnak nevezzük. Ha valószínűségek a megelőző eseményektől függnek, akkor Markov - folyamatnak nevezzük. A hírközlés szempontjából ezen belül is a ergodius folyamatok különösen fontosak. Tegyük fel, hogy két személy eltérő módon választ ki mintákat és tanulmányozzuk, hogy e minták statisztikai tulajdonságai milyen trendet mutatnak, ha a minták növekszenek. Ha a szituáció ergodikus, akkor a két személy bárhogyan is választotta ki a mintáját, egészében véve a sajátosságok becslésében megegyezik.
A termodinamika második törvénye a világegyetemben állandóan növekvő rendezetlenségre, az entrópiára vonatkozik. Shannon, az entrópiát az információval azonosítva, a szónak új, az eredetivel ellentétes jelentést adott. Az entrópia növekedése az információ növekedését eredményezi. A pillanatnyi és a maximális entrópia viszonyát a forrás relatív entrópiájának nevezzük. Különbségük pedig a belső entrópia:

Az egy mínusz relatív entrópia a redundancia. Ez az a része az üzenetnek, amelyet nem az adó szabad választása határoz meg, hanem a szimbólumok használatának elfogadott statisztikus törvényszerűségei szabályoznak. Az üzenet ez a része szükségtelen abban az értelemben, hogy ha a redundáns rész hiányozna, akkor az üzenet még mindig teljes, vagy legalábbis teljessé tehető. Így az információra kapott kifejezés:

ahol p a kiválasztási valószínűség.
A hírközlési elméletben a csatorna kapacitása nagy fontosságú az átvitt információ mennyiségét illetően. Ha a forrás olyan, hogy minden egyes kiválasztott szimbólum s bitnyi információt hordoz, és a csatorna másodpercenként n szimbólumot képes átvinni, akkor a csatorna kapacitása a következőképpen írható fel:

Shannon tétele kimondja, hogy a csatornában továbbított üzenet sebessége sohasem haladhatja meg a C/H értéket, bármilyen módon is kódolja az adó az üzenetet.
A forrás által kibocsátott üzenet nem kívánatos (járulékos) bizonytalanságát (vagyis a zaj okozta bizonytalanságot) ekvivokációnak nevezzük.
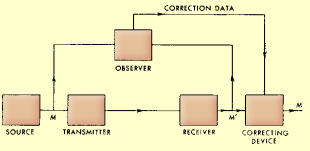
A B. szintnek tehát ezt a járulékos bizonytalanságot is figyelembe kell venni, vagyis olyan szemantikai kódolást kell használnia, mely kiküszöböli a zaj okozta jelentéstorzulást. Shannon ezzel részletesen nem foglalkozik, mert vizsgálata tárgya nem az egyes egyedi üzenetek vizsgálata, hanem egy teljes üzenetegyüttes statisztikus jellege, valamint a zajnak, mint jelenségnek a vizsgálata. Ehhez a vizsgálathoz kapcsolódik az a korrekciós vázlata, melyben a fentebb látható kommunikációs modellt kiegészíti úgy, hogy a zaj okozta járulékos bizonytalanságot kiküszöbölje, vagy legalábbis minimálisra csökkentse.

Az elmélet kapcsolata más elméleti konstrukciókkal:
Shannon elmélet nem előzmények nélküli. Az elektronikus kommunikációs rendszerekben történő információ mennyiség- és sebesség mérésével már R. V. L. Hartley is foglalkozott. Ő fogalmazta meg elsőként, hogy az adó a rendelkezésére álló jelkészletbol rendre jeleket választ ki, s azokból sorozatokat, "üzeneteket" állít össze. Az információ mennyiségét tizes alapú logaritmusban számolta ki, a kapott eredményt pedig hartleyban (mértékegység) kapta meg.
Alig néhány évvel a shannoni elmélet megszületése után D.M. MacKay kidolgozta a tudományos információ elméletét. Eszerint az ember ismereteit képzetek - absztrakt vagy valós struktúrák, képek, sémák, modellek - formájában tárolja. Képzeteit a befogadó az információk segítségével alakítja ki vagy módosítja. Kétféleképpen juthatnak információhoz: fizikai megfigyelés és mérés útján, vagy kommunikációs folyamatban. Előbbi új képességeket hoz létre, utóbbi során reprodukáljuk azokat a képzeteket, amelyekkel az adó már előzőleg rendelkezett (MacKay, 1952).
Az induktív logika felől közelíti meg a szemantikai információ mennyiségét Y. Bar-Hillel és L. Carnap. Elméletük "tulajdonképpen a Shannon-féle elméletnek pontos logikai képe". Egy állítás információtartalmának mérésére bevezetik a tartalmi mértéket. (content measure = cont). Ha egy i állítás logikai valószínűsége (pl. a hipotézis megerősítésének foka)
mi, akkor cont i = l-mi. Bar-Hillel megjegyzi: "A nyelvi rendszerek, amelyekre információel-méletünket kidolgoztuk, nagyon egyszerűek". Ebben a kijelentésben implicite már benne van elméletük kritikája is. "A szemantikai információnak lényegéből következően semmi köze a kommunikációhoz", majd egy másik helyen: "Mi azt az információt vizsgáljuk, amelyet egy mondat hordoz, önmagában vagy más mondatokhoz viszonyítva, de nem foglalkozunk azzal az információval, amelyet a feladó szándékozott küldeni egy bizonyos üzenet továbbításával, vagy amit a vevő kapott az üzenetből." (Bar -Hillel - Carnap, 1956, Bar-Hillel, 1955, 1964).

Az elmélet-alkotás célja:
Távközlési rendszerek, illetve technikai rendszerek problémamentes adattovábbítása, az adott rendszer engedte maximális sebességgel. Cél, hogy a jelek egy meghatározott csatornán olyan sebességgel haladjanak, hogy a maximális sávszélességet használják ki úgy, hogy az átvitel során fellépő zajok ne befolyásolják a jelentést, vagyis a vevőoldalon a fogadott jel ne, vagy csak minimális mértékben torzuljon az eredetihez képest.

Az elmélet eredeti alkalmazási terepe:
A távközlés, technikai rendszerek (diszkrét, folytonos, ill. vegyes) jeltovábbítása, kommunikációja zajos és teljesen zajmentes csatornákon.

Az elmélet háttérdiszciplínái:
Matematika, fizika, informatika.

Néhány fontosabb bibliográfiai tétel:
Claude E. Shannon - Warren Weaver: A kommunikáció matematikai elmélete.
OMIK. Budapest. 1986.
Szász Gábor-Kun István-Zsigmond Gyula: Kommunikációs rendszerek
LSI. Budapest. 1999.

Az összefoglalót készítette:
Barkóczy László
Dátum: 2003. január 10.